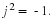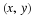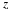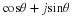We use this chapter to introduce students to the algebraic structure of vectors and matrices and to introduce them to matrix computations. These matrix computations are used in the chapters "Vector Graphics", "Filtering", and "Binary Codes" to solve problems in vector graphics, filtering, and binary coding.

Vectors are introduced in the section "Vectors", along with algebraic and geometric interpretations of some fundamental vector operations and properties. The section "Inner Product and Euclidean Norm", the section "Direction Cosines", and the section "Projections" introduce inner products and their applications, including norm, direction cosines, orthogonality, and projections. Some important alternatives to the Euclidean norm are introduced in the section "Other Norms". Matrices are motivated and introduced in this section. The notation in these sections can be daunting to the beginner, so we proceed very carefully, using example after example. In the section "Solving Linear Systems of Equations" we codify the elimination procedures that students have used in high school to solve linear systems of equations. The MATLAB demonstration in Demo 2 shows how to use MATLAB to solve linear equations. The section "Circuit Analysis" shows how linear algebra and MATLAB can be used to analyze dc circuits. The numerical experiment "Circuit Design" gives students practice in building function files in MATLAB and shows how to solve a sequence of linear equations in order to design a circuit with desired properties.

Occasionally we have placed important results in the problems. We feel that students should not miss the material in Exercise 3 in "Vectors", Exercise 3 in "Inner Product and Euclidean Norm", Exercise 3 in "Projections", Exercise 1 in "Matrices", and Exercise 4 in "Matrices".

Introduction

Linear algebra is a branch of mathematics that is used by engineers and applied scientists to design and analyze complex systems. Civil engineers use linear algebra to design and analyze load-bearing structures such as bridges. Mechanical engineers use linear algebra to design and analyze suspension systems, and electrical engineers use it to design and analyze electrical circuits. Electrical, biomedical, and aerospace engineers use linear algebra to enhance X rays, tomographs, and images from space. In this chapter and the next we study two common problems from electrical engineering and use linear algebra to solve them. The two problems are (i) electrical circuit analysis and (ii) coordinate transformations for computer graphics. The first of these applications requires us to understand the solution of linear systems of equations, and the second requires us to understand the representation of mathematical operators with matrices.

Much of linear algebra is concerned with systematic techniques for organizing and solving simultaneous linear equations by elimination and substitution. The following example illustrates the basic ideas that we intend to develop.

Example 4.1. 

A woman steps onto a moving sidewalk at a large airport and stands while the moving sidewalk moves her forward at 1.2 meters/seconds. At the same time, a man begins walking against the motion of the sidewalk from the opposite end at 1.5 meters/second (relative to the sidewalk). If the moving sidewalk is 85 meters long, how far does each person travel (relative to the ground) before they pass each other?

To solve this problem, we first assign a variable to each unknown quantity. Let x₁ be the distance traveled by the woman, and let x₂ be the distance traveled by the man. The sum of the two distances is 85 meters, giving us one equation:

(4.1) x₁ + x₂ = 85 .

Our second equation is based on the time required before they pass. Time equals distance divided by rate, and the time is the same for both people:

(4.2)

We may substitute Equation 4.2 into Equation 4.1 to obtain the result , or

(4.3) 5 x₂ = 85 ⇒ x₂ = 17 .

Combining the result from Equation 4.3 with that of Equation 4.1, we find that

(4.4) x₁ = 68 .

So the man travels 17 meters, and the woman travels 68 meters.

Equation 4.1 and Equation 4.2 are the key equations of Equation 4.1. They may be organized into the “matrix equation”

(4.5)

The rules for matrix-vector multiplication are evidently

(4.6)

(4.7) ( 0 . 3 ) x₁ + ( – 1 . 2 ) x₂ = 0 .

Equation 4.2 and Equation 4.3 may be organized into the matrix equation

(4.8)

This equation represents one partially solved form of Equation 4.5, wherein we have used the so-called Gauss elimination procedure to introduce a zero into the matrix equation in order to isolate one variable. The MATLAB software contains built-in procedures to implement Gauss elimination on much larger matrices. Thus MATLAB may be used to solve large systems of linear equations.

Before we can apply linear algebra to more interesting physical problems, we need to introduce the mathematical tools we will use.

For our purposes, a vector is a collection of real numbers in a one- dimensional array.^[6] We usually think of the array as being arranged in a column and write

.

Notice that we indicate a vector with boldface and the constituent elements with subscripts. A real number by itself is called a scalar, in distinction from a vector or a matrix. We say that x is an n-vector, meaning that x has n elements. To indicate that x₁ is a real number, we write

meaning that x₁ is contained in R, the set of real numbers. To indicate that x is a vector of n real numbers, we write

meaning that x is contained in Rⁿ, the set of real n-tuples. Geometrically, Rⁿis n-dimensional space, and the notation x∈Rⁿ means that x is a point in that space, specified by the n coordinates x₁,x₂,...,x_n. Figure 4.1 shows a vector in R³, drawn as an arrow from the origin to the point x . Our geometric intuition begins to fail above three dimensions, but the linear algebra is completely general.

Figure 4.1. 

A Vector in R³

We sometimes find it useful to sketch vectors with more than three dimensions in the same way as the three-dimensional vector of Figure 4.1. We then consider each axis to represent more than one dimension, a hyperplane, in our n-dimensional space. We cannot show all the details of what is happening in n-space on a three-dimensional figure, but we can often show important features and gain geometrical insight.

Vector Addition. Vectors with the same number of elements can be added and subtracted in a very natural way:

(4.11)

Figure 4.2. 

Subtraction of Vectors

Scalar Product. Several different kinds of vector multiplication are defined.^[7] We begin with the scalar product. Scalar multiplication is defined for scalar a and vector x as

(4.12)

If |a|<1, then the vector ax is "shorter" than the vector x; if |a|>1, then the vector ax is ‚"longer" than x. This is illustrated for a 2-vector in Figure 4.3.

Figure 4.3. 

The Scalar Product ax

The inner product (x,y) between vectors x and y is a scalar consisting of the following sum of products:

This definition seems so arbitrary that we wonder what uses it could possibly have. We will show that the inner product has three main uses:

Since the inner product is so useful, we need to know what algebraic operations are permitted when we are working with inner products. The following are some properties of the inner product. Given x,y,z∈Rⁿ and a∈R,

Euclidean Norm. Sometimes we want to measure the length of a vector, namely, the distance from the origin to the point specified by the vector's coordinates. A vector's length is called the norm of the vector. Recall from Euclidean geometry that the distance between two points is the square root of the sum of the squares of the distances in each dimension. Since we are measuring from the origin, this implies that the norm of the vector x is

(4.14)

Notice the use of the double vertical bars to indicate the norm. An equivalent definition of the norm, and of the norm squared, can be given in terms of the inner product:

(4.15)

or