(s)
sols #
sols #
(kbytes)
MSSM
octahedron
T,P
T,P
0,07
16
16
60
TSSM
hexapod
S,P
T,P
0,08
16
16
76
SSM
(6|)
S,P
S,P
0,67
36
16
238
6-6pp
(6|)
P
P
1,1
40
16
390
6-6p
(6|)
NP
P
1,8
40
16
308
6-6
(6|)
NP
NP
10,4
40
16
402
DIET
(6|)
NP
NP
9,9
40
40
392
Hexa
6R-6R-6R
P
S,P
2,0
40
8
346
Hexaglide
6T-6R-6R
P
S,P
0,5
36
8
180
Table 5. Hexapod FKP overall results and performances
6.6.3 Discussion on the results
The gradual passage to geometrically simpler parallel structures leads to significantly
shorter response times. In the 6-6 case, the introduction of one planar platform reduces
computation times by 20. Inasmuch, the passage from a theoretical SSM to a realistic 6-6
leads to computation times which are 40 times longer.

Certified Solving and Synthesis on Modeling of the Kinematics. Problems of Gough-Type
Parallel Manipulators with an Exact Algebraic Method
201
With model simplification, it is notable that the real solution number is maintained. One
could conjecture homothopy in those cases. The number of complex roots varies when the
manipulator type changes; the MSSM and TSSM only have 16 solutions whereas the SSM
has 36. This last result raises an important classification issue which was not formerly
identified, [Faugère and Lazard 1995, Merlet 1997]. The SSM manipulator does not go in the
class of 6-6 manipulators and becomes a class by itself.
The table second section comprises FKP solving results about the hexapod obtained with the
Dietmaier's method, [Dietmaier 1998], the Hexa and the Hexaglide with a SSM type mobile
platform. In all instances, the Hexa, [Pierrot et al. 1991], and Hexaglide, [Hebsacker 1998]
can feature either 36 or 40 complex solutions, this only depends on the mobile platform
configuration. In fact, when the truncated equilateral triangle is used, then the FKP yield 36
solutions.
Knowing that the 6-6pp and 6-6p lead to 40 complex solutions, the new SSM class is
characterized not only by its complex solution number but by the mobile platform and fixed
base peculiar type.
Therefore, the manipulators which fall into the SSM category are the ones which feature one
specific truncated platform.
Although Dietmaier's 6-6 FKP yields the largest number of real solutions, it does not
necessarily lead to the longest computation times and largest result files.
Finally, various tests were performed where leg lengths were changed such as moving the
robot on a straight line or circles with the same 6-6 manipulator configuration. The real root
numbers have all been an even number in the set {4,8,12,16} depending on the location
inside the workspace. This could be considered a conjecture. The only case where only one
real solution has been found is when a theoretical 6-6pp has its actuator values bringing the
manipulator mobile platform to lie on the fixed base plane. This solution corresponds to two
real coincident roots and this case can be identified as a singularity with the loss of three
DOF since the manipulator can then only move in a plane.
6.7 Assembly mode analyses
The exact method allows addressing the question of assembly modes. This problem is also
referred to as posture analysis. Assembly modes are defined as follows:
Fig. 12. Posture analysis for the general 6-6 manipulator
202
Parallel Manipulators, Towards New Applications
Definition 6.1 Given a manipulator configuration where the fixed base, the mobile platform and
kinematics chain lengths are specified, for a set of active joint positions, determine all the possible
geometric assemblies for the selected manipulator.
For the selected example, eight real solutions were obtained which geometrically represent
the only possible assembly modes. These modes are then drafted using the XMuPAD
environment, fig. 12. The position based models lead to root results which are directly
usable to draw the effective postures. This exemplifies that posture analysis is feasible for
any manipulator which can be modelled as a general 6-6 hexapod.
7. Conclusion
In this chapter, one complete exact method to solve the parallel manipulator FKP has been
explained. The method was applied to the 6-6 general parallel manipulator, which is
recognized to yield the most difficult problem, and also to various other manipulators such
as the SSM, TSSM, MSSM, Hexa and Hexaglide.
Moreover, the modeling of the FKP was investigated. Six displacement based models and
two position-based models were derived for the 6-6 general parallel manipulator.
One complete algebraic method to solve the Forward Kinematics Problem was applied.
Although many methods can find solutions to some of these FKP systems, the proposed
algebraic exact method insures the exactness of the real solution results, since it is based on
one Gröbner Basis, which completely describes the ideal related to the original system. From
this basis, one computes the Rational Univariate Representation including one univariate
equation for root isolation. The selected algorithms always succeeded to solve any parallel
robot FKP in all tested non-singular instances.
The selected manipulator was a typical 6-6 hexapod known as the Gough platform in a
calibrated configuration, measured on a real parallel robot prototype constructed from a
theoretically singularity free SSM design.
The 8 polynomial formulations were implemented and compared. We identified three
models that allowed for computation termination, out of which two were retained since
their computations occur with acceptable performances: a displacement based formulation
with the rotation matrix Gröbner Basis with end-effector position and rotation matrix
parameters as variables and a formulation with three points on a platform.
Solving typical posture examples, the Rational Univariate Representation comprised a
univariate equation of degree 40 and 8 to 12 real solutions were computed depending on the
position in the workspace. The total computation averaged 130 seconds on a relatively old
computer. On a faster computer, the response time falls to less than one second. Hence, this
method can be suitable for small-scale trajectory pursuit applications.
This result is very important since any Gröbner Basis completely describes the mathematical
object related to the original system. From this basis, one can try to build an exact equivalent
system with the original one including one univariate equation. Up to author’s knowledge,
this is actually the only known method that is certified to establish a truly equivalent system
that preserves the properties.
Further testing led to favor the first formulation, since it yields slightly faster computations
and it gives directly the end-effector position. The quaternion-based models can lead to
difficulties in the case of simpler configurations and thus longer computation times, since it
is doubling the solution number, which is explained by the Rational Univariate Representation
Certified Solving and Synthesis on Modeling of the Kinematics. Problems of Gough-Type
Parallel Manipulators with an Exact Algebraic Method
203
equations having a degree twice as large as the others. Moreover, one final advantage is that
the displacement-based equations can be applied on any manipulator mobile platform.
8. Acknowledgment
I would like to thank my wife Clotilde for the time spent on rewriting and correcting the
book chapter in Word.
9. References
Alonso, M.-E.; Becker, E.; Roy M.F. & Woermann T. (1996) Multiplicities and idempotents
for zerodimensional systems. In Algorithms in Algebraic Geometry and Applications,
Vol. 143, Progress in Mathematics, pages 1--20.
Buchberger, B. & Loos, R. (1982) Algebraic Simplification. In Computer Algebra-Symbolic and
Algebraic Computation. SpringerVerlag, Vienna.
Buchberger B. (1985) Gröbner bases: An Algorithmic Method in Polynomial Ideal Theory. In
Multidimensional Systems Theory – Progress, Directions and Open Problems in
Multidimensional Systems, N.K. Bose (e.d.) Reidel Publishing Company, Dordrecht,
pp.184-232.
Bruyninckx, H. & DeSchutter, J. (1996) A class of fully parallel manipulators with closed-
form forward position kinematics. In Advances in Robot Kinematics, pages 411--420.
Cox, D.; Little, J. & O'Shea D. (1992) Ideals, varieties, and algorithms an introduction to
computational algebraic geometry and commutative algebra. Undergraduate texts in
mathematics. SpringerVerlag, New York.
Dedieu, J.P. & Norton, G.H. (1990) Stewart varieties: a direct algebraic method for stewart
platforms. In Proceedings of SigSam, volume 244, pages 42--59.
P. Dietmaier. (1998) The Stewart-Gough platform of general geometry can have 40 real
postures. In Advances in Robot Kinematics, pages 7--16.
Dieudonné, E.; Parrish, R. & Bardusch, R. (1972) An actuator extension transformation for a
motion simulator and an inverse transformation applying Newton-Raphson`s
method. Technical report D7067, NASA, Washington.
Didrit, O.; Petitot, M. & Walter, E. (1998) Guaranteed solution of direct kinematics problems
for general configurations of parallel manipulators. IEEE Transactions on Robotics
and Automation, Vol. 14, No. 2, pages 259--265.
Egner, S. (1996) Semi-numerical solution to 6/6-stewart-platform kinematics based on
symmetry. In Applicable Algebra in Engineering, Communication and Computing, Vol.
7, No. 6, pages 449--468.
Faugère, J.-C.; Gianni, P.; Lazard, D. & Mora, T. (1991) Efficient computation of zero-
dimensional Gröbner basis by change of ordering . Journal of Symbolic Computation,
Vol. 16, No. 4, pages 329--344.
Faugère, J.C. & D. Lazard. (1995) The combinatorial classes of parallel manipulators.
Mechanism and Machine Theory, Vol. 30, No. 6, pages 765--776.
Faugère, J.C. (1999) A new efficient algorithm for computing Gröbner bases (f4). J. of Pure
and Applied Algebra, Vol. 139, No. 13, pages 61--88.
Fischer, P.J. & Daniel, R.W. (1992) Real time kinematics for a 6 dof telerobotic joystick. In
Proceedings of RoManSy 9, Udine, pages 292--300.
204
Parallel Manipulators, Towards New Applications
Geddes, K.; Czapor, S. & Labahn, G. (1994) Algorithms for computer algebra. Kluwer Academic
Publishers, Nonwell.
Gosselin, C. & Angeles, J. (1988) The optimum kinematic design of a planar three dof
parallel manipulator. J. of Mechanisms, Transmissions and Automation in Design, Vol.
110, pages 35--41.
Gosselin, C.; Sefrioui, J. & Richard, M.J. (1994) On the direct kinematics of spherical three
dof parallel manipulators with coplanar platform. J. of Mechanical Design, Vol. 116,
pages 587--593, June 1994.
Griffis, M. & Duffy, J. (1989) A forward displacement analysis of a class of stewart platform.
J. of Robotic Systems, Vol. 6, No. 6, pages 703--720.
Hebsacker, M. (1998) Parallel werkzeugmaschinenkinematik. In Proceedings of IPK 98,
Internationales ParallelkinematikKolloquium, Zürich, pages 21--32.
Hunt, K.H. (1983) Structural kinematics of inparallelactuated robotarms. J. of Mechanisms,
Transmissions and Automation in Design, Vol. 105, pages 705--712.
Husty, M. (1996) An algorithm for solving the direct kinematic of Stewart-Gough type
platforms. J. of Mechanism and Machine Theory, Vol. 31, No. 4, pages 365--379, 1996.
Innocenti, C. & ParentiCastelli, V. (1990) Direct position analysis of the Stewart platform
mechanism. Mechanism and Machine Theory, Vol. 25, No. 6, pages 611-- 621.
Kohli, D.; Dhingra, A. & Xu, Y.X. (1992) Direct kinematics of general Stewart platforms. In
Proceedings of ASME Conference on Robotics, Spatial Mechanisms and Mechanical
Systems, Vol. 45, pages 107--112.
Lazard, D. (1992) Solving zerodimensional algebraic systems. J. of Symbolic Computation, Vol.
13, pages 117--131.
Lazard, D. (1992) Stewart platforms and Gröbner basis. In Proceedings of Advances in Robotics
Kinematics, pages 136--142, Ferrare, September 1992.
Lazard, D. (1993) On the representation of rigidbody motions and its application to
generalized platform manipulators. J. of Computational Kinematics, Vol. 1, No. 1,
pages 175--182.
Merlet, J.-P. (1987) Parallel manipulators, part1: Theory; design, kinematics, dynamics and
control. Technical report 646, INRIA, SophiaAntipolis.
Merlet, J.-P. (1994) Parallel manipulators: state of the art and perspectives. J. of Advanced
Robotics, Vol. 8, No. 6, pages 589--596, 1994.
Merlet, J.-P. (1997) Les Robots parallèles. Série Robotique. Hermès, Paris, second edition, traité
des nouvelles technologies edition, 1997.
Merlet, J.-P. (2004) Solving the forward kinematics of a Goughtype parallel manipulator
with interval analysis. The International Journal of Robotics Research, Vol. 23, No. 3,
pages 221--235.
Mourrain, B. (1993) The 40 generic positions of a parallel robot. In proceedings of ISSAC'93,
Kiev, pages 173--182.
Mourrain, B. (1993) About the rational map associated to a parallel robot. Technical report
2141, INRIA, SophiaAntipolis, November 1993.
Murray, P.; et al. (1997) A planar quaternion approach to the kinematics synthesis of a
parallel manipulator. Robotica, Vol. 15, pages 360--365.
Nanua, P.; Waldron, K. T& Murthy, V. (1990) Direct kinematic solution of a Stewart
platform . In IEEE transactions on Robotics and Automation, Vol. 6, No.4, pages 438-
444.
Certified Solving and Synthesis on Modeling of the Kinematics. Problems of Gough-Type
Parallel Manipulators with an Exact Algebraic Method
205
ParentiCastelli, V. & Innocenti, C. (1990) Forward displacement analysis of parallel
mechanisms: closedform solution of PRR3s and PPR3s structures. In Proceedings of
the ASME 21th Biennial Mechanisms Conf., Chicago, pages 263--269.
Patel, A. & Ehmann, K. (1997) Volumetric error analysis of a Stewart platform based
machine tool. In Annals of the CIRP, Vol. 46, pages 287--290.
Petuya, V.; Alonso, A.; Altazurra, O. & Hernandez, A. (2005) Resolution of the direct
position problem of the parallel kinematic platforms using the geometric iterative
method. In EEE Intern. Conf. on Robotics and Automation, Barcelona, pages 3255--
3260.
Pierrot, F.; Dauchez, F. & Fournier, A. (1991) Hexa: a fast six dof fully parallel robot. In
Proceedings of the ICAR Conference, Pisa, pages 1159--1163.
Primrose, E.J.F. & Freudenstein, F. (1969) Spatial motions. part 1: Point paths of mechanisms
with four or fewer links. ASME J. of engineering for industry, Vol. 91, No. 1, pages
103-- 114.
Raghavan, M. (1993) The stewart platform of general geometry has 40 configurations. ASME
Trans. of Mech. Design, Vol. 115, No. 2, pages 277--282.
Raghavan, M. & Roth, B. (1995) Solving polynomial systems for the kinematic analysis and
synthesis of mechanisms and robot manipulators. Transactions of the ASME, Vol.
117, pages 71--79.
Rolland, L. (2003) Outils algébriques pour la résolution de problèmes géométriques et
l'analyse de trajectoire de robots parallèles prévus pour des applications à haute
cadence et grande précision. PhD thesis, Université Henri Poincaré, Nancy 1,
December 2003.
Rolland, L. (2005) Certified solving of the forward kinematics problem with an exact method
for the general parallel manipulator. Advanced Robotics, Vol. 19, No. 9, pages 995--
1025.
Rolland, L. (2006) Synthesis on the forward kinematics problem algebraic modeling for the
planar parallel manipulator. Displacement-based equation systems. Advanced
Robotics, Vol. 20, No. 9, pages 1035--1065.
Rolland, L. (2007) Synthesis on the forward kinematics problem algebraic modeling for the
spatial parallel manipulator. Displacement-based equation systems. Advanced
Robotics, Vol. 21, No. 9, 32 pages 1071--1092.
Ronga, F. & Vust, T. (1992) Stewart platforms without computer ? In Proc. of the Intern. Conf.
of real, analytic and algebraic Geometry, Trento, pages 197--212.
Rouillier, F. (1999) Solving zerodimensional systems through the rational univariate
representation. Journal of Applicable Algebra in Engineering, Communication and
Computing, Vol. 9, NO. 5, pages 433--461.
Rouillier, F. & Zimmermann, P. (2001) Efficient isolation of a polynomial real roots.
Technical report RR4113, INRIA.
Sreenivasan, S.V. & Nanua, P. (1992) Solution of the direct position kinematics problem of
the general stewart platform using advanced polynomial continuation. In 22nd
Biennial Mechanisms Conf. , Scottsdale, pages 99--106.
Sreenivasan, S.V.; Waldron, K.J. & Nanua, P. (1994) Direct displacement analysis of a 6-6
stewart platform. Mechanism and Machine Theory, Vol. 29, No. 6, pages 855--864.
206
Parallel Manipulators, Towards New Applications
Sugimoto, K. (1987) Kinematic and dynamic analysis of parallel manipulators by means of
motor algebra . J. of Mechanisms, Transmissions and Automation in Design, Vol. 109:
pages 3--7, 1987.
Tsai, L.W. & Morgan, A.P. (1984) Solving the kinematics of the most general 6 and 5 dof
manipulators by continuation methods. ASME J. of Mechanisms, Transmissions and
Automation in Design, Vol. 107, pages 189--200.
Vischer, P. (1996) Improving the accuracy of parallel robots. PhD thesis, Ecole Polytechnique
Fédérale de Lausanne.
Wampler, C.W. (1996) Forward displacement analysis of general six-in-parallel SPS
(Stewart) platform manipulators using soma coordinates. Mechanism and Machine
Theory, Vol. 31, NO. 3, pages 33--337.
10
Advanced Synthesis of the DELTA Parallel
Robot for a Specified Workspace
M.A. Laribi1, L. Romdhane1* and S. Zeghloul2
Laboratoire de Génie Mécanique, LAB-MA-05
Ecole Nationale d’Ingénieurs de Sousse, Sousse 40031,
Laboratoire de Mécanique des Solides,UMR 6610
Bd Pierre et Marie Curie, BP 30179,Futuroscope 86962 Chasseneuil2
Tunisia1,
France2
1. Introduction
Parallel manipulators have numerous advantages in comparison with serial manipulators:
Higher stiffness, and connected with that a lower mass of links, the possibility of
transporting heavier loads, and higher accuracy. The main drawback is, however, a smaller
workspace. Hence, there exists an interest for the research concerning the workspace of
manipulators.
Parallel architectures have the end-effector (platform) connected to the frame (base) through
a number of kinematic chains (legs). Their kinematic analysis is often difficult to address.
The analysis of this type of mechanisms has been the focus of much recent research. Stewart
presented his platform in 1965 [1]. Since then, several authors [2],[3] have proposed a large
variety of designs.
The interest for parallel manipulators (PM) arises from the fact that they exhibit high
stiffness in nearly all configurations and a high dynamic performance. Recently, there is a
growing tendency to focus on parallel manipulators with 3 translational DOF [4, 5, 8, 9, 10,
11, 12, 13,]. In the case of the three translational parallel manipulators, the mobile platform
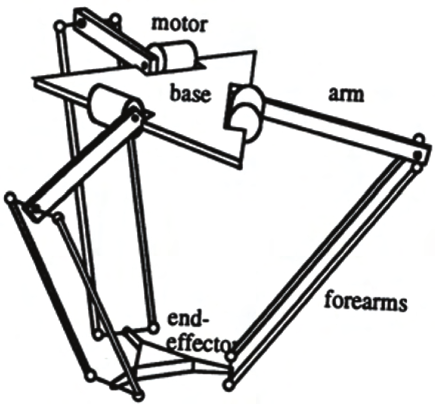
can only translate with respect to the base. The DELTA robot (see figure 1) is one of the most
famous translational parallel manipulators [5,6,7]. However, as most of the authors
mentioned above have pointed out, the major drawback of parallel manipulators is their
limited workspace. Gosselin [14], separated the workspace, which is a six dimensional
space, in two parts : positioning and orientation workspace. He studied only the positioning
workspace, i.e. , the region of the three dimensional Cartesian space that can be attained by a
point on the top platform when its orientation is given. A number of authors have described
the workspace of a parallel mechanism by discretizing the Cartesian workspace. Concerning
the orientation workspace, Romdhane [15] was the first to address the problem of its
determination. In the case of 3-Translational DOF manipulators, the workspace is limited to
* Corresponding author. email :lotfi.romdhane@enim.rnu.tn
208
Parallel Manipulators, Towards New Applications
a region of the three dimensional Cartesian space that can be attained by a point on the
mobile platform.
Fig. 1: DELTA Robot (Clavel R. 1986)
A more challenging problem is designing a parallel manipulator fo





