Conditions: q
+ q
< b q
> b + q
q
> b + q
1 min
2 min
, 1 max
2 min ,
2 max
1 min
Fig. 22. The workspace of the planar 2 DOF Parallel Kinematics Machine is shown as the
shading region.
Case VI:
Conditions: q
+ q
> b q
> b + q
q
> b + q
1 min
2 min
, 1 max
2 min ,
2 max
1 min
Fig. 23. The workspace of the planar 2 DOF Parallel Kinematics Machine is shown as the
shading region.
Case VII:
Conditions:
q
< b
q
<
q
<
q
<
q
+ q
<
1 min
,
b
1 max
,
b
2 min
,
b
2 max
,
b
1 min
2 min
,
q
+ q
> b
1 max
2 max
Fig. 24. The workspace of the planar 2 DOF Parallel Kinematics Machine is shown as the
shading region.
312
Parallel Manipulators, Towards New Applications
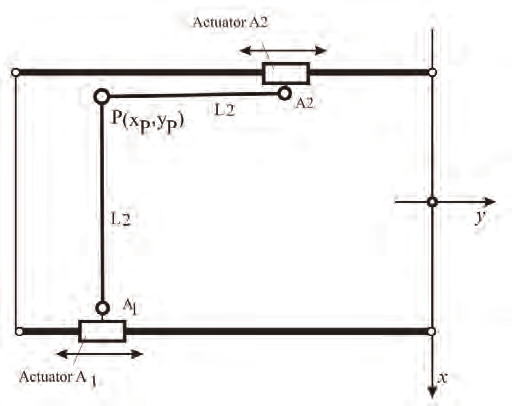
In the followings is presented the workspace analysis of 2 DOF Biglide Parallel Kinematics
Machine.
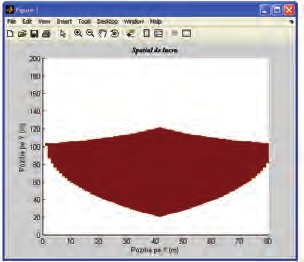
a) Workspace for the planar 2 DOF Parallel Kinematics Machine, case
q
= q
=100 mm
1 max
2 max
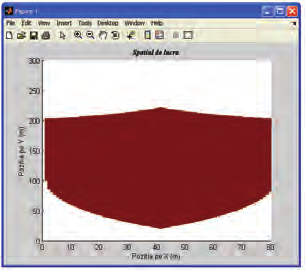
b) Workspace for the planar 2 DOF Parallel Kinematics Machine, case
q
= q
= 200 mm
1 max
2 max
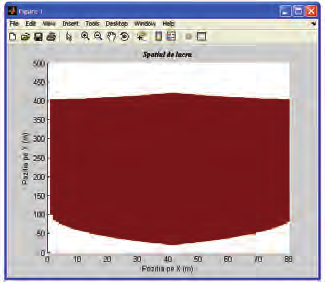
c) Workspace for the planar 2 DOF Parallel Kinematics Machine, case
q
= q
= 400 mm
1 max
2 max
Fig. 25. Different regions of workspace for Biglide PKM for different lengths of stroke of
actuators

Optimal Design of Parallel Kinematics Machines with 2 Degrees of Freedom
313
4.2 Singularity analysis of the Biglide Parallel Kinematics Machine
Because singularity leads to a loss of the controllability and degradation of the natural
stiffness of manipulators, the analysis of parallel manipulators has drawn considerable
attention. Most parallel robots suffer from the presence of singular configurations in their
workspace that limit the machine performances. Based on the forward and inverse Jacobian
matrix, three cases of singularities of parallel manipulators can be obtained. Singular
configurations should be avoided.
In the followings are presented the singular configurations of 2 DOF Biglide Parallel
Kinematic Machine.
Fig. 26. Singular configuration for the planar 2 DOF Biglide Parallel Kinematic Machine
Fig. 27. Singular configuration for the planar 2 DOF Biglide Parallel Kinematic Machine

314
Parallel Manipulators, Towards New Applications
Fig. 28. Singular configuration for the planar 2 DOF Biglide Parallel Kinematic Machine
4.2 Performance evaluation
Beside workspace which is an important design criterion, transmission quality index is
another important criterion. The transmission quality index couples velocity and force
transmission properties of a parallel robot, i.e. power features (Hesselbach et al., 2004). Its
definition runs:
2
I
T =
(9)
1
−
J ⋅ J
where I is the unity matrix. T is between 0<T<1; T=0 characterizes a singular pose, the
optimal value is T=1 which at the same time stands for isotropy (Stan, 2003).
MAX=
Übertragungsgüte
0.658553
MIN=
0.427955
0.64
MWT=
0.62
0.8 0.503084
0.6
0.7
0.58
0.56
0.6
0.54
0.5
0.52
0.5
0.4
0
0.48
0
50
0.46
50
100
100
0.44
150 150
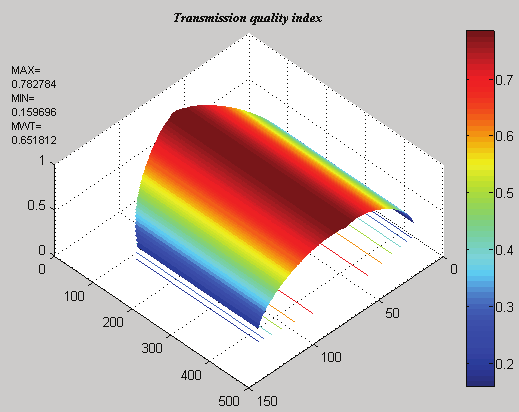
Fig. 29. Transmission quality index for RPRPR Bipod Parallel Kinematic Machine
Optimal Design of Parallel Kinematics Machines with 2 Degrees of Freedom
315
Fig. 30. Transmission quality index for PRRRP Biglide Parallel Kinematic Machine
As it can be seen from the Fig. 30, the performances of the PRRRP Biglide Parallel Kinematic
Machine are constant along y-axis. On every y section of such workspace, the performance
of the robot can be the same.
5. Optimal design of 2 DOF Parallel Kinematics Machines
5.1 Optimization results for RPRPR Parallel Kinematic Machine
The design of the PKM can be made based on any particular criterion. The chapter presents
a genetic algorithm approach for workspace optimization of Bipod Parallel Kinematic
Machine. For simplicity of the optimization calculus a symmetric design of the structure was
chosen.
In order to choose the PKM’s dimensions b, q1min, q1max, q2min, q2max, we need to define a performance index to be maximized. The chosen performance index is W (workspace) and T
(transmission quality index).
An objective function is defined and used in optimization. It is noted as in Eq. (8), and
corresponds to the optimal workspace and transmission quality index. We can formalize our
design optimization problem as the following:
ObjFun=W+T
(10)
Optimization problem is formulated as follows: the objective is to evaluate optimal link
lengths which maximize Eq. (10). The design variables or the optimization factor is the ratios
of the minimum link lengths to the base link length b, and they are defined by:
q1min/b
(11)
316
Parallel Manipulators, Towards New Applications
Constraints to the design variables are:
0,52<q1min/b<1,35
(12)
q1min=q2min, q1max=q2max, q1max=1,6q1min, q2max=1,6q2min
(13)
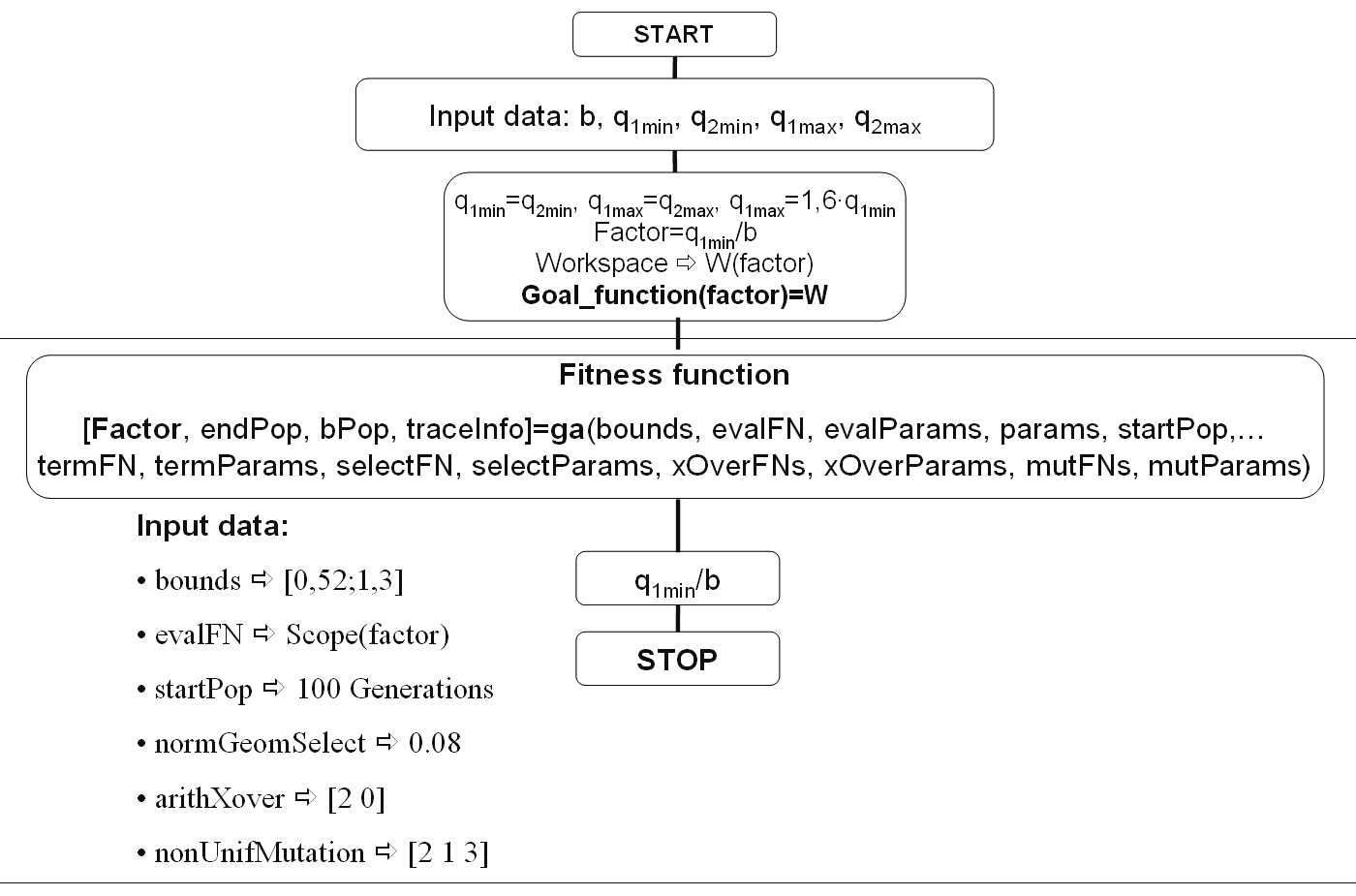
Fig. 31. Flowchart of the optimization Algorithm with GAOT (Genetic Algorithm
Optimization Toolbox)
For this example the lower limit of the constraint was chosen to fulfill the condition q1min≥b/2
that means the minimum stroke of the actuators to have a value greater than the half of the
distance between them in order to have a workspace only in the upper region. For simplicity
of the optimization calculus the upper bound was chosen q1min≤1,35b.
During optimization process using genetic algorithm it was used the following GA
parameters, presented in Table 1.
Generations 100
Crossover rate
0.08
Mutation rate
0.005
Population 50
Table 1. GA Parameters
Researchers have used genetic algorithms, based on the evolutionary principle of natural
chromosomes, in attempting to optimize the design parallel kinematics. Kirchner and
Neugebaur (Kirchner & Neugebaur, 2000), emphasize that a parallel manipulator machine
tool cannot be optimized by considering a single performance criterion. Also, using a
Optimal Design of Parallel Kinematics Machines with 2 Degrees of Freedom
317
genetic algorithm, they consider a multiple design criteria, such as the “velocity
relationship” between the moving platform and the actuator legs, the influence of actuator
leg errors on the accuracy of the moving platform, actuator forces, stiffness, as well as a
singularity-free workspace.
A genetic algorithm (GA) is used because its robustness and good convergence properties.
The genetic algorithms optimization approach has the clear advantage over conventional
optimization approaches in that it allows a number of solutions to be examined in a single
design cycle.
The traditional methods searches optimal points from point to point, and are easy to fall into
local optimal point. Using a population size of 50, the GA was run for 100 generations. A list
of the best 50 individuals was continually maintained during the execution of the GA,
allowing the final selection of solution to be made from the best structures found by the GA
over all generations.
We performed a kinematic optimization in such a way to maximize the objective function. It
is noticed that optimization result for Bipod when the maximum workspace of the 2 DOF
planar PKM is obtained for q
/ b
1
=1,35. The used dimensions for the 2 DOF parallel
min
PKM were: q1min=80 mm, q1max=130 mm, q2min=80 mm, q2max=130 mm, b=60 mm. Maximum
workspace of the Parallel Kinematics Machine with 2 degrees of freedom was found to be
W= 4693,33 mm2.
If an elitist GA is used, the best individual of the previous generation is kept and compared
to the best individual of the new one. If the performance of the previous generation’s best
individual is found to be superior, it is passed on to the next generation instead of the
current best individual.
There have been obtained different values of the parameter optimization ( q1/b) for different
objective functions. The following table presents the results of optimization for different
goal functions. W1 and W2 are the weight factors.
Method
GAOT Toolbox MATLAB
Z=W1·T+W2·W, W1=0,7
q
and W
1/b = 0.92
2=0,3
Z=W1·T+W2·W, W1=0,3
q
Goal functions
and W
1/b= 1.13
2=0,7
Z= W1·T,
q
W
1/b=0.71
1=1 and W2=0
Z=W2·W,
q
W
1/b= 1.3
1=0 and W2=1
Table 2. Results of Optimization for Different Goal Functions
The results show that GA can determine the architectural parameters of the robot that
provide an optimized workspace. Since the workspace of a parallel robot is far from being
intuitive, the method developed should be very useful as a design tool.
However, in practice, optimization of the robot geometrical parameters should not be
performed only in terms of workspace maximization. Some parts of the workspace are more
useful considering a specific application. Indeed, the advantage of a bigger workspace can
318
Parallel Manipulators, Towards New Applications
be completely lost if it leads to new collision in parts of it which are absolutely needed in the
application. However, it’s not the case of the presented structure.
5.2 Optimization results for PRRRP Parallel Kinematic Machine
An objective function is defined and used in optimization. Objective function contains
workspace and transmission quality index. Optimization parameter was chosen as the link
length L2. The constraints was established as 1<L2<1.2. After performing the optimization
the following results were obtained:
Method
GAOT Toolbox MATLAB
Z=W1·T+W2·W, W1=0,7
L
and W
2 = 1.1
2=0,3
Z=W1·T+W2·W, W1=0,3
L
and W
2= 1.1556
2=0,7
Goal functions
Z= W1·T,
L
W
2=1
1=1 and W2=0
Z=W2·W,
L
W
2=1.2
1=0 and W2=1
Table 3. Results of Optimization for Different Goal Functions
Based on the presented optimization methodology we can conclude that the optimum
design and performance evaluation of the Parallel Kinematics Machines is the key issue for
an efficient use of Parallel Kinematics Machines. This is a very complex task and in this
paper was proposed a framework for the optimum design considering basic characteristics
of workspace, singularities and isotropy.
6. Conclusion
The fundamental guidelines for genetic algorithm to optimal design of micro parallel robots
have been introduced. It is concluded that with three basic generators selection, crossover
and mutation genetic algorithm could search the optimum solution or near-optimal solution
to a complex optimization problem of micro parallel robots. In the paper, design
optimization is implemented with Genetic Algorithms (GA) for optimization considering
transmission quality index, design space and workspace. Genetic algorithms (GA) are so far
generally the best and most robust kind of evolutionary algorithms. A GA has a number of
advantages. It can quickly scan a vast solution set. Bad proposals do not affect the end
solution negatively as they are simply discarded. The obtained results have shown that the
use of GA in such kind of optimization problem enhances the quality of the optimization
outcome, providing a better and more realistic support for the decision maker.
7. References
Agrawal, S. K., (1990). Workspace boundaries of in-parallel manipulator systems. Int. J.
Robotics Automat. 1990, 6(3) 281-290.
Optimal Design of Parallel Kinematics Machines with 2 Degrees of Freedom
319
Cecarelli, M., (1995). A synthesis algorithm for three-revolute manipulators by using an
algebraic formulation of workspace boundary. ASME J. Mech. Des. ; 117(2(A)): 298-
302.
Ceccarelli, M., G. Carbone, E. Ottaviano, (2005). An Optimization Problem Approach For
Designing Both Serial And Parallel Manipulators, In: Proc. of MUSME 2005, the
International Symposiom on Multibody Systems and Mechatronics, Uberlandia, Brazil, 6-
9 March 2005.
Ceccarelli, M., (2004). Fundamentals of Mechanics of Robotic Manipulation, Dordrecht,
Kluwer/Springer.
Cleary, K. and Arai, T. (1991). A prototype parallel manipulator: Kinematics, construction,
software, workspace results, and singularity analysis. In: Proceedings of International
Conference on Robotics and Automation, pages 566–571, Sacramento, California, USA,
April 1991.
Davidson, J. K. and Hunt, K. H., (1987). Rigid body location and robot workspace: some
alternative manipulator forms. ASME Journal of Mech. Transmissions Automat Des,
109(2); 224-232.
Du Plessis L.J. and J.A. Snyman, (2001). A numerical method for the determination of
dextrous workspaces of Gough-Stewart platforms. Int. Journal for Numerical Methods
in Engineering, 52:345–369.
Ferraresi, C., Montacchini, G. and M. Sorli, (1995). Workspace and dexterity evaluation of 6
d.o.f. spatial mechanisms, In: Proceedings of the ninth World Congress on the theory of
Machines and Mechanism, pages 57–61, Milan, August 1995.
Gogu, G., (2004), Structural synthesis of fully-isotropic translational parallel robots via
theory of linear transformations, European Journal of Mechanics, A/Solids, vol. 23, pp.
1021-1039.
Gosselin, C. (1990). Determination of the workspace of 6-d.o.f. parallel manipulators. ASME
Journal of Mechanical Design, 112:331–336.
Gosselin, C., and Angeles J. (1990). Singularities analysis of closed loop kinematic chains.
IEEE Trans Robotics Automat; 6(3) 281-290.
Gupta, K. C. (1986). On the nature of robot workspaces, International Journal of Robotics
Research. 5(2): 112-121.
Gupta, K. G. and Roth B., (1982). Design considerations for manipulator workspace. ASME J.
Mech. Des. , 104(4), 704-711.
Hesselbach, J., H. Kerle, M. Krefft, N. Plitea, (2004). The Assesment of Parallel Mechanical
Structures for Machines Taking Account of their Operational Purposes. In:
Proceedings of the 11th World Congress in Mechanism and Machine Science-IFToMM 11,
Tianjin, China, 2004.
Kirchner, J., and Neugebauer, R., (2000). How to Optimize Parallel Link Mechanisms –
Proposal of a New Strategy. In: Proceedings Year 2000 Parallel Kinematics Machines
International Conference, September 13-15, 2000, Ann Arbor, Mi. USA, [Orlandea, N.
et al. (eds.)], pp. 307-315.
Kumar, A. and Waldron, (1981). K.J. The workspace of mechanical manipulators. ASME J.
Mech. Des.; 103:665-672.
Masory, O. and Wang J. (1995). Workspace evaluation of Stewart platforms.
Advanced robotics, 9(4):443-461.
320
Parallel Manipulators, Towards New Applications
Merlet, J. P., (1995). Determination of the orientation workspace of parallel manipulators.
Journal of intelligent and robotic systems, 13:143–160.
Pernkopf, F. and Husty, M., (2005). Reachable Workspace and Manufacturing Errors of
Stewart-Gough Manipulators, Proc. of MUSME 2005, the Int. Sym. on Multibody
Systems and Mechatronics Brazil, p. 293-304.
Schoenherr, J., (1998). Bemessen Bewerten und Optimieren von Parallelstrukturen, In: Proc.
1st Chemnitzer Parallelstruktur Seminar, Chemnitz, Germany, 85-96.
Snyman, J. A., L.J. du Plessis, and J. Duffy. (2000). An optimization approach to the
determination of the boundaries of manipulator workspaces. Journal of Mechanical
Design, 122:447–455.
Stan, S., (2003). Analyse und Optimierung der strukturellen Abmessungen von
Werkzeugmaschinen mit Parallelstruktur, Diplomarbeit, IWF-TU Braunschweig,
Germany.
Stan, S., (2006). Workspace optimization of a two degree of freedom mini parallel robot,
IEEE-TTTC International Conference on Automation, Quality and Testing, Robotics –
AQTR 2006 (THETA 15), May 25-28 2006, Cluj-Napoca, Romania, IEEE Catalog
number: 06EX1370, ISBN: 1-4244-0360-X, pp. 278-283.
Stan, S. and Lăpuşan, C., (2006). Workspace analysis of a 2 dof mini parallel robot, The 8th
National Symposium with International Participation COMPUTER AIDED DESIGN -
PRASIC'06, Braşov, 9 - 10th November 2006, pag. 175-180, ISBN (10)973-653-824-0;
(13)978-973-635-824-1.
Stan, S., Vistrian M., Balan, R. (2007). Optimal Design of a 2 DOF Micro Parallel Robot Using
Genetic Algorithms, Proceedings of the 2007 IEEE-ICIT 2007, IEEE International
Conference on Integration Technology, March 20 - 24, 2007, Shenzhen, China, 1-4244-
1092-4/07, p. 719-724, IEEE Catalog Number: 07EX1735, ISBN: 1-4244-1091-6, ISBN:
1-4244-1092-4.
Stan, S., Balan, R., Vistrian M., (2007). Multi-objective Design Optimization of Mini Parallel
Robots Using Genetic Algorithms, IEEE-ISIE 2007 2007 IEEE International
Symposium on Industrial Electronics, June 4-7, 2007, Caixanova - Vigo, Spain, IEEE
Catalog Number: 07TH8928C, ISBN: 1-4244-0755-9, Library of Congress:
2006935487, pag. 1-4244-0755-9/07/ IEEE 2173-2178.
Stan, S., Maties, V., Balan, R., (2007). Optimization of 2 DOF Micro Parallel Robots Using
Genetic Algorithms, IEEE-ICM 2007, IEEE - International Conference on Mechatronics
2007, 8-10 May, 2007, Kumamoto, Japan, ISBN: 1-4244-1184-X
IEEE Catalog Number of CD proceedings: 07EX1768C, ISBN of CD












