Angeles, J. (2005). The degree of freedom of parallel robots: a group-theoretic approach,
Proceedings of IEEE International Conference on Robotics and Automation, pp. 1017-
1024, Barcelona, Spain, April 2005
Basu, D. & Ghosal, A. (1997). Singularity analysis of platform-type multi-loop spatial
mechanisms. Mechanism and Machine Theory, Vol. 32, No. 3, pp. 375-389
Benov, I. (2001). Delta parallel robot – the story of success. May, 6,
http://www.parallemic.org/Reviews/Review002.html
Bonev, L. & Zlatanov, D. (2001). The mystery of the singular SUN translational parallel
robot. June, 12, 2001, http://www.parallemic.org/Reviews/Review004.html
Bonev, I.A. et al. (2001). A closed-form solution to the direct kinematics of nearly general
parallel manipulators with optimally located three linear extra sensors. IEEE
Transaction on Robotics and Automation, Vol. 17, No. 2, pp. 148-156
Bottema, O. & Roth, B. (1990). Theoretical kinematics. New York: Dover Publications
Brogardh, T. PKM research – important issues, as seen from a product development
perspective at ABB robotics, Workshop on Fundamental Issues and Future Research
Directions for parallel Mechanisms and Manipulators, Quebec, Canada, 2002
444
Parallel Manipulators, Towards New Applications
Bruyninckx, H. (1997). The 321-hexa: a fully parallel manipulator with closed-form position
and velocity kinematics, Proceedings of IEEE Conference on Robotics and Automation,
pp. 2657-2662, Albuquerque, April, 1997
Carretero, J.A.; Podhorodeski, R.P.; Nahon, M.A. & Gosselin, C.M. (2000). Kinematic
analysis and optimization of a new three degree-of-freedom spatial parallel
manipulator. ASME Journal of Mechanical Design, Vol. 122, pp. 17-24
Chablet D, D.; Wenger, P. Design of a three-axis isotropic parallel manipulator for
machining applications: the orthoglide, Workshop on Fundamental Issues and Future
Research Directions for Parallel Mechanisms and Manipulators, Quebec, Canada, Oct.,
2002
Cheung, J.W.F.; Hung, Y.S. & Widdowson, G.P. (2002). Design and analysis of a novel 4-dof
parallel manipulator for semiconductor applications, Proceedings of the 8th
Mechatronics Forum International Conference, pp. 1358-1366, Twente, Netherlands:
Drebbel Institute for Mechatronics
Chiu, Y.J. & Perng, M-H. (2001). Forward kinematics of a general fully parallel manipulator
with auxiliary sensors. International Journal of Robotics Research, Vol. 20, No. 5, pp.
401-414
Choi, H.-B.; Konno, A. & Uchiyama, M. (2003). Closed-form solutions for the forward
kinematics of a 4-DOFs parallel robot H4, Proceedings of IEEE/RSJ International
Conference on Intelligent Robots and Systems, pp. 3312-3317, Las Vegas, USA, October,
2003
Clavel, R. (1988). DELTA, a fast robot with parallel geometry, Proceedings of the 18th
International Symposium on Industrial Robot, pp. 91-100, April, 1988, Lausanne
Collins, C.L. & Long, G.L. (1995). The singularity analysis of an in-parallel hand controller
for force-reflected teleoperation. IEEE Transactions on Robotics and Automation, Vol.
11, No. 5, pp. 661-669
Company, O. & Pierrot, F. (1999). A new 3T-1R parallel robot, Proceedings of the 9th
International Conference on Advanced Robotics, pp. 557-562, October, 1999, Tokyo,
Japan
Company, O.; Marquet, F. & Pierrot F. (2003). A new high-speed 4-DOF parallel robot
synthesis and modeling issues. IEEE Transactions on Robotics and Automation, Vol.
19, No. 3, pp. 411-420
Company, O.; Pierrot, F. & Fouroux, J.C. (2005). A method for modeling analytical stiffness
of a lower mability parallel manipulator, Proceedings of IEEE International Conference
on Robotics and Automation, pp. 18-22, Barcelona, Spain, April, 2005, Milan,
September, 1995
Di Gregorio, R. & Parenti-Castelli, V. (1999). Mobility analysis of the 3-UPU parallel
mechanism assembled for a pure translational motion, Proceedings of the
IEEE/ASME International Conference on Advanced Intelligent Mechatronics, pp. 520-
525, Atlanta, GA, September, 1999
Fattah, A. & Kasaei, G. (2000). Kinematics and dynamics of a parallel manipulator with a
new architecture. Robotica, Vol. 18, pp. 535-543
A Novel 4-DOF Parallel Manipulator H4
445
Faugère, J.C. & Lazard, D. (1995). The combinatorial classes of parallel manipulators.
Mechanism and Machine Theory, Vol. 30, No. 6, pp. 765-776
Feng-Cheng, Y. & Haug, E.J. (1994). Numerical analysis of the kinematic working capability
of mechanism. ASME Journal of Mechanical Design, Vol. 116, pp. 111-117
Funabashi, H. & Takeda, Y. (1995). Determination of singular points and their vicinity in
parallel manipulators based on the transmission index, Proceedings of the Ninth
World Congress on the Theory of Machine and Mechanism, pp. 1977-1981,
Gosselin, C.M. & Angeles, J. (1989). The optimum kinematic design of a spherical three-
degree-of-freedom parallel manipulator. ASME Journal of Mechanisms, Transmission
and Automation in Design, Vol.111, No.2, pp. 202-207
Gosselin, C. & Angeles, J. (1990). Singularity analysis of closed-loop kinematic chains. IEEE
Transaction on Robotics and Automation, Vol. 6, No. 3, pp. 281-290
Gosselin, C. (1990). Dexterity indices for planar and spatial robotic manipulators. Proceedings
of the IEEE International Conference on Robotics and Automation, pp. 650-655,
Cincinnati, May, 1990
Gosselin, C. (1996). Parallel computational algorithms for the kinematics and dynamics of
planar and spatial parallel manipulators. A SME Journal of Dynamic Systems,
Measurement and Control, Vol. 118, No. 1, pp. 22-28
Gosselin, C.M. & St-Pierre, É. (1997). Development and experimentation of a fast 3-DOF
camera-orienting device. The International Journal of Robotics Research, Vol.16, No.5,
pp. 619-629
Gough, V.E. (1956). Contribution to discussion of papers on research in automobile stability,
control and tyre performance, Proceedings of the Automotive Division of the Institution
of Mechanical Engineers, Part D, pp. 392-394
Gregorio, R. D. (2001). A new parallel wrist using only revolute pairs: the 3-RUU wrist.
Robotica, Vol. 19, pp. 305-309
Hao, F. McCarthy, J.M. (1998). Conditions for line-based singularities in spatial platform
manipulators. Journal of Robotic Systems, Vol. 15, No. 1, pp. 43-55
Hesselbach, J. & Kerle, H. (1995). Structurally adapted kinematic algorithms for parallel
robots up to six degrees if freedom (dof), Proceedings of the 9th World Congress on the
Theory of Machines and Mechanisms, pp. 1935-1939, Milan, Italy, August, 1995
Hunt, K.H. (1978). Kinematic geometry of mechanism. Department of Mechanical
Engineering, Monash University, Clayton, Victoria, Australia
Husty, M.L. (1996). On the workspace of planar three-legged platforms. Proceedings of the
World Automation Congress, Vol. 3, pp. 339-344, Montpellier, May, 1996
Jo, D.Y. & Haug, E.J. (1989). Workspace analysis of closed loop mechanism with unilateral
constraints. Proceedings of the ASME Design Automation Conference, pp. 53-60,
Montreal, September, 1989
Joshi, S.A. & Tsai L.-W. (2002) Jacobian analysis of limited-dof parallel manipulators. ASME
Journal of Mechanical Design, Vol. 124, No. 2, pp. 254-258
446
Parallel Manipulators, Towards New Applications
Kim, D.; Chung, W. & Youm, Y. (2000). Analytic jacobian of in-parallel manipulators.
Proceedings of IEEE International Conference on Robotics and Automation, pp. 2376-
2381, San Francisco, April, 2000
Kim, S.-G. & Ryu, J. (2003). New dimensionally homogeneous jacobian matrix formulation
by three end-effector points for optimal design of parallel manipulators. IEEE
Transactions on Robotics and Automation, Vol. 19, No. 4, pp. 731-736
Krut, S.; Company, O. &Benoit, M. et al. (2003). I4: a new parallel mechanism for scara
motions, Proceedings of IEEE International Conference on Robotics and Automation, pp.
1875-1880, Taipei, Taiwan, September, 2003
Krut, S.; Nabat, V.; Company, O. & Pierrot, F. (2004). A high-speed parallel robot for scara
motions, Proceedings of IEEE International Conference on Robotics and Automation, pp.
4109-4115, New Orleans, USA, April, 2004
Li, Q. & Huang, Z. (2003). Mobility analysis of lower-mobility parallel manipulators based
on screw theory, Proceeding of IEEE International Conference on Robotics and
Automation, pp. 1179-1184, Taipei, Taiwan, September, 2003
Liu, G.F.; Lou, Y.J. & Li, Z.X. (2003). Singularities of parallel manipulators: a geometric
treatment. IEEE Transactions on Robotics and Automation, Vol. 19, No. 4, pp. 579-594
Merlet, J.P. (1992). On the infinitesimal motion of a parallel manipulator in singular
configurations, Proceedings of IEEE International Conference on Robotics and
Automation, pp. 320-325, Nice, France, May, 1992
Merlet, J.-P. (2000). Kinematics’ not dead, Proceedings of IEEE International Conference on
Robotics & Automation, pp. 1-6, San Francisco, CA, April, 2000
Merlet, J.-P. & Daney, D. (2005). Dimensional synthesis of parallel robots with a guaranteed
given accuracy over a specific workspace, Proceedings of IEEE International
Conference on Robotics and Automation, pp. 19-22, Barcelona, Spain, April, 2005
Merlet, J.-P. (2006). Parallel Robots (Second Edition), Springer, Dordrecht, The Netherlands
Nabat, V.; Company, O. & Krut, M. et al. (2005). Part 4: very high speed parallel robot for
pick-and-place, Proceedings of IEEE International Conference on Intelligent Robots and
Systems, pp. 553-558, Edmonton, Canada, August, 2005
Nabat, V.; Company, O. & Pierrot, F. (2006). Dynamic modeling and identification of Part 4,
a very high speed parallel manipulator, Proceedings of the International Conference on
Intelligent Robots and Systems, pp. 496-501, Beijing, China, October, 2006
Parenti-Castelli, P. & Di Gregorio, P. (20010). Real-time actual pose determination of the
general fully parallel spherical wrist, using only one extra sensor. Journal of Robotic
Systems, Vol. 18, No. 12, pp. 723-729
Pennock, G.R. & Kassner, D.J. (1990). Kinematic analysis of a planar eight-bar linkage:
application to a platform-type robot, ASME Proceedings of the 21th Biennial
Mechanism Conference, pp. 37-43, Chicago, September, 1990
Pierrot, F. & Company, O. (1999). H4: a new family of 4-dof parallel robots, Proceedings of the
1999 IEEE/ASME International Conference on Advanced Intelligent Mechatronics, pp.
508-513, Atlanta, USA, September, 1999
A Novel 4-DOF Parallel Manipulator H4
447
Pottmann, H.; Peternell, M. & Ravani, B. (1999). An introduction to line geometry with
applications. Compter Aided Design, Vol. 31, pp. 3-16
Reboulet, C. & Robert, A. (1985). Hybrid control of a manipulator with an active compliant
wrist, The 3rd International Symposium of Robotics Research, pp. 76-80, Gouvieux,
France, October, 1985
Renaud, P.; Andreff, N. & Marquet, F. et al.. (2003). Vision-based kinematic calibration of a
H4 parallel mechanism. Proceedings of the IEEE International Conference on Robotics &
Automation, pp. 1191-1196, Taipei, Taiwan, September, 2003
Robotics Department of LIRMM. H4 with rotary drives: a member of H4 family, dedicated
to high speed applications.
http://www.lirmm.fr/w3rob/SiteWeb/detail_resultat.php?num_resultat=7&num
_topic=1& num_projet=1&num_activite=3
Rolland, L. The manta and the kanuk: novel 4-dof parallel mechanisms for industrial
handling. ASME Dynamic Systems and Control Division, IMECE’99 Conference, pp.
831-844, Nashville, USA, November 1999
Romdhane, L.; Affi, Z. & Fayet, M. (2002). Design and singularity analysis of a 3-
translational-DOF in-parallel manipulator. ASME Journal of Mechanical Design, Vol.
124, pp. 419-426
Ryu, J. & Cha, J. (2003). Volumetric error analysis and architecture optimization for accuracy
of HexaSlide type parallel manipulators. Mechanism and Machine Theory, Vol. 38, pp.
227-240
Steward, D. (1965). A platform with 6 degrees of f reedom. Proceedings of the Institution of
Mechanical Engineers, Vol. 180, Part 1, No. 15, pp. 371-386, British
St-Onge, B.M. & Gosselin, C.M. (2000). Singularity analysis and representation of the general
Gaugh-Steward platform. International Journal of Robot Research, Vol.19, No. 3, pp.
271-288
Su, Y.X.; Duan, B.Y. & Peng, B. et al.. (2003). Singularity analysis of fine-tuning stewart
platform for large radio telescope using genetic algorthm. Mechatronics, Vol. 13, pp.
413-425
Tsai, L.-W. (1996). Kinematics of a three-DOF platform with three extensible limbs. Recent
Advances in Robot Kinematics, Kluwer Academic Publishers, pp. 401-410
Tsai, L.-W. & Joshi, S.A. (2000). Kinematics and optimization of a spatial 3-UPU parallel
manipulators. A SME Journal of Mechanical Design, Vol. 122, No.4, pp. 439-446
Wolf, A. & Shoham, M. (2003). Investigation of parallel manipulators using linear complex
approximation. ASME Journal of Mechanical Design, Vol. 125, No. 3, pp. 564-572
Wu, J.; Yin, Z. & Xiong, Y. (2006). Singularity analysis of a novel 4-dof parallel manipulator
H4. International Journal of Advanced Manufacturing and Technology, Vol. 29, pp. 794-
802
Zlatanov, D.; Fenton, R.G. & Benhabit, B. (1994). Singularity analysis of mechanism and
robots via a motion-space model of the instantaneous kinematics. Proceedings of
IEEE International Conference on Robotics and Automation, pp. 980-991, San
Diego, CA, May, 1994
448
Parallel Manipulators, Towards New Applications
Zlatanov, D.; Benov, I.A. & Gosselin, C.M. (2002). Constraint singularities of parallel
mechanisms, Proceedings of the IEEE International Conference on Robotics and
Automation, pp. 496-502, Washington DC, May, 2002
Zobel, P.B., Di Stefano, P. & Raparelli, T. (1996). The design of a 3 dof parallel robot with
pneumatic dirves, Proceedings of the 27th International Symposium on Industrial Robot,
pp. 707-710, October, 1996, Milan
20
Human Hand as a Parallel Manipulator
Vladimir M. Zatsiorsky ad Mark L. Latash
Department of Kinesiology, The Pennsylvania State University
1. Introduction
When a human hand grasps an object the hand can be viewed as a parallel manipulator. In
general, the mathematical analyses of the human hands and multi-fingered robot hands
(Murray et al. 1994) are similar. In particular, concepts developed in robotics such as contact
models, e.g. soft-finger model, grasp matrix, form and force closure grasps, internal forces,
etc. can be applied to analyze the performance of the human hands. Multi-finger prehension
is an example of a mechanically redundant task: the same resultant forces on the object can
be exerted by different digit forces. People however do not use all the mechanically
available options; when different people perform a certain manipulation task they use a
limited subset of solutions.
Studies on human prehension deal with four main issues:
1. Description of the behavior: What are the regularities in force patterns applied at the
fingertip-object interfaces when people manipulate objects?
2. Are the observed patterns dictated by the task and hand mechanics? The mechanical
properties of the hand and fingers are complex, and it is not always evident whether the
findings are direct consequences of the mechanical properties of the hand or they are
produced by a neural control process.
3. If the observed facts/phenomena are not of mechanical origin are they mechanically
necessitated? In other words, can the task be performed successfully in another way?
4. If reproducible phenomena are not mechanical and not mechanically-necessitated, the
question arises why the central nervous system (CNS) facilitates these particular
phenomena. This is a central question of the problem of motor redundancy in general:
Why does the CNS prefer a certain solution over other existing solutions?
The present chapter briefly reviews some specific features of the human hand and the
involved control mechanisms. To date, the experimental data are mainly obtained for the so-
called prismatic grasps in which the thumb opposes the fingers and the contact surfaces are
parallel (Figure 1). The contact forces and moments are typically recorded with 6-
component force and moment sensors.
Experimental ‘inverted-T’ handle/beam apparatus commonly used to study the prismatic
precision grip. Five six-component force sensors (black rectangles) are used to register
individual digit forces. During testing, the suspended load could vary among the trials. The
load displacement along the horizontal bar created torques from 0 N⋅m to 1.5 N⋅m in both
directions. The torques are in the plane of the grasp. While forces in all three directions were
recorded the forces in Z direction were very small and, if not mentioned otherwise, were
450
Parallel Manipulators, Towards New Applications
neglected. When the handle is oriented vertically the force components in the X and Y
directions are the normal and shear, (or tangential) forces, respectively. The figure is not
drawn to scale.
60 mm
Y
Z
Index
X
30 mm
Thumb
Middle
30 mm
Ring
30 mm
Little
Torque 0.0-1.5 Nm
Load 0.5 kg
Figure 1. Experimental ‘inverted-T’ handle/beam apparatus
2. Digit contacts
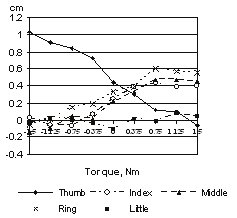
During an object manipulation the finger tips deform and the contact areas are not constant
(Nakazawa et al. 2000; Paré et al. 2002; Serina et al. 1997; Srinivasan, 1989; Srinivasan et al.
1992; Pataky et al. 2005). The fingers can also roll on the sensor surface. As a result, the point
of digit force application is not constant: it can displace by up to 5-6 mm for the fingers and
up to 11-12 mm for the thumb (Figure 2). Therefore the digit tip contacts should be as a rule
treated as the soft-finger contacts (Mason & Salisbury, 1985).
When a soft-finger model of the digit-object contact is employed, the contact is characterized
by six variables: three orthogonal force components (the normal force component is uni-
directional and the two tangential force components are bi-directional), free moment in the
plane of contact, and two coordinates of the point of force application on the sensor. To
obtain these data the six-component force and moment sensors are necessary. The
coordinates of the point of force application are not recorded directly; they are computed
from the values of the normal force and the moment around an axis in the contact plane.
Such a computation assumes that the fingers do not stick to the sensor surfaces, in other
words the fingers can only push but not pull on the sensors. In such a case the moment of
force about the sensor center is due to the application of the resultant force at a certain
distance from the center. The displacements of the points of digit force application change
the moment arms of the forces that the digits exert on the hand-held object and make the
computations more cumbersome.
Human Hand as a Parallel Manipulator
451
Figure 2. Displacement of the point of application of digit forces in the vertical direction at
the various torque levels. The results are for an individual subject (average of ten trials). The
positive direction of the torque is counterclockwise (pronation efforts), the negative
direction is clockwise (supination efforts). Adapted by permission from V.M. Zatsiorsky, F.
Gao, and M.L. Latash. Finger force vectors in multi-finger prehension. Journal of
Biomechanics, 2003a, 36:1745-1749.
3. Hand asymmetry and hierarchical prehension control
Asymmetry in the hand function is an important feature that differentiates the hand from
many parallel manipulators used in engineering as well as from some robotic hands (Fu &
Pollard 2006). The functional hand asymmetry is in part due to the hand design (e.g. the
thumb opposing other fingers, differences in the capabilities of index and little fingers, etc.)
and in part is due to the hand control.
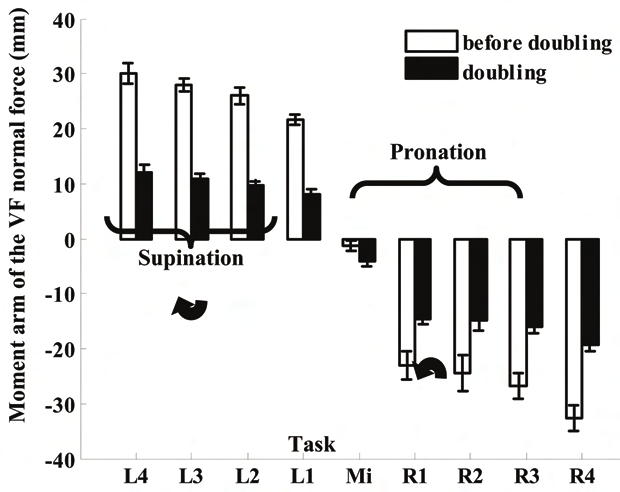
Due to the specific function of the thumb opposing other fingers in grasping, the forces of
the four fingers can be reduced to a resultant force and a moment of force. This is
equivalent to replacing a set of fingers with a virtual finger, VF (Arbib et al. 1985, Iberall 1987;
Baud-Bovy & Soechting, 2001). A VF generates the same wrench as a set of actual fingers.
There are substantial differences between the forces exerted by individual fingers (IF) and
VF forces: (a) The IF force directions are as a rule dissimilar (for a review see Zatsiorsky &
Latash 2008) while their resultant (i.e., VF) force is in the desired direction (Gao et al. 2005).
(b) VF and IF forces adjust differently to modifications in task conditions (Zatsiorsky et al.
2002a, b). (c) IF forces are much more variable than VF forces (Shim et al. 2005a, b). The
desired performance at the VF level is achieved by a synergic co-variation among individual
finger forces at the IF level. The above facts support a hypothesis that multi-finger
prehension is controlled by a two-level hierarchical control scheme (reviewed in Arbib et al.
1985; Mackenzie & Iberall 1994). At the upper level, the required mechanical action on the
object is distributed between the thumb and the VF. At the lower level, action of the VF is
distributed among individual fingers.
452
Parallel Manipulators, Toward





