Load (N)
Figure 10. Tangential forces of the thumb and VF in the three-digit grasps as a function of
the load and friction, high (H) or low (L). The eight friction conditions were HHH, HLL,
HHL, HLH, LLL LHH, LHL, and LLH, where the letters correspond to the friction condition
462
Parallel Manipulators, Towards New Applications
for the thumb, index and middle fingers, respectively. The friction sets with the thumb at a
low friction contact (LLL, LHH, LHL and LLH) are printed with dotted lines. The solid lines
represent the tasks with the high friction contact at the thumb. In the left panel, LFE is the
local friction effect , i.e. the difference induced by the high or low friction contact at the thumb.
Two other smaller figure brackets show the synergic effects, i.e. the effect of friction at other
digits on the thumb force. The numbers in the bottom right insets are the regression
coefficients and intercepts (the regression model t
)
1
(
f = a + k
.
L
i
i
i
was used for
computations). Note the small values of the intercepts. Cf. the right and the left panels: the
thumb friction, H or L, induced opposite changes of the thumb and VF forces. (The figure is
from X. Niu, M. Latash, V.M. Zatsiorsky (2007) Prehension synergies in minimally
redundant grasps & the triple-product model of digit force control, Experimental Brain
Research, 98 (1): 16-28.)
Local and synergic reactions are not limited to adjustments to local friction. For instance,
similar reactions were observed when performers were holding a motorized handle while
the handle width was forcibly either increased or decreased (Zatsiorsky et al. 2006). Handle
expansion/contraction did not perturb the handle equilibrium; both the resultant force and
moment acting on the handle remained the same. However, when the handle width
increased each digit was perturbed (the length of the flexor muscle increased), and a
restoring force tending to return the digit to its previous position arose (the local digit force
adjustment). The local mechanisms, e.g. stretch reflexes, were directed to resist the imposed
digit displacement. These mechanisms violated the object equilibrium, whilst the synergic
force adjustments restored the equilibrium.
9. Principle of superposition in human prehension
The principle of superposition refers to decomposition of complex skilled actions into several
elemental actions, which can be controlled independently by several controllers. The
principle was first suggested in robotics (Arimoto et al. 2001; Arimoto & Nguyen 2001) and
was verified for the dexterous manipulation of an object by two soft-tip robot fingers. Such a
control can be realized via a linear superposition of two commands, one command for the
stable grasping and the second one for regulating the orientation of the object. In robotics,
such a decoupled control decreases the computation time.
When applied to multi-finger grasps in humans, the principle claims that at the VF level the
forces and moments during prehension are defined by two independent commands: “Grasp
the object stronger/weaker to prevent slipping” and “Maintain the rotational equilibrium of
the object”. The commands correspond to the two internal forces discussed previously, the
grip force and the internal moment. The effects of the two commands are summed up. The
validity of the principle was confirmed in a set of diverse experiments (for the review see
Zatsiorsky et al. 2004; see also Shim et al. 2005 and Shim & Park, 2007)). The principle allows
explaining the digit force adjustments to different factors such as (a) the load force and its
modulation associated with the handle acceleration; (b) the external torque and its
modulation; (c) the object orientation in the gravity field; (c) friction at the digit tips; and
some other variables. The variations of the above factors may require similar or opposite
adjustments. For instance, an increase of the object weight and a decrease in friction both
require a larger gripping force while, a decrease of the load and a decrease in friction require
opposite grasp force changes, a force decrease and increase, respectively. It has been
Human Hand as a Parallel Manipulator
463
suggested that the CNS responds to a mixture of similar or opposite requirements follows a
rule: Adjustment to the sum equals the sum of the adjustments (reviewed in Zatsiorsky& Latash
2008).
10. References
Aoki, T.; Latash, M. L., and Zatsiorsky, V. M. (2007). Adjustments to local friction in
multifinger prehension. J Mot Behav. Jul; 2007. 39(4):276-90.
Aoki, T.; Niu, X.; Latash, M. L., and Zatsiorsky, V. M. (2006) Effects of friction at the digit-
object interface on the digit forces in multi-finger prehension. Exp Brain Res . 2006
Jul; 172(4):425-38.
Arbib MA; Iberall T, and Lyons D. (1985) Coordinated control programs for movements of
the hand. Goodwin AW and Darian-Smith I , eds. Hand Function and the Neocortex .
Berlin: Springer Verlag; 1985; pp. 111-129.
Arimoto, S. and Nguyen, P. T. A. (2001) Principle of superposition for realising dexterous
pinching motions of a pair of robot fingers with soft-tips. IEICE Transactions on
Fundamentals of Electronics Communications and Computer Sciences. 2001 Jan;
E84A(1):39-47.
Arimoto, S.; Tahara, K.; Yamaguchi, M.; Nguyen, P. T. A., and Han, H. Y. (2001) Principles
of superposition for controlling pinch motions by means of robot fingers with soft
tips. Robotica . 2001 Jan-2001 Feb 28; 19:21-28.
Baud-Bovy, G. and Soechting, J. F. (2001) Two virtual fingers in the control of the tripod
grasp. J Neurophysiol . 2001 Aug; 86(2):604-15.
Danion, F.; Schoner, G.; Latash, M. L.; Li, S.; Scholz, J. P., and Zatsiorsky, V. M. (2003) A
mode hypothesis for finger interaction during multi-finger force- production tasks.
Biol Cybern. 2003 Feb; 88(2):91-8.
Flanagan, J. R.; Tresilian, J., and Wing, A. M. (1993) Coupling of grip force and load force
during arm movements with grasped objects. Neurosci Lett. 1993 Apr; 152(1-2):53-6.
Flanagan, J. R. and Tresilian, J. R. (1994) Grip-load force coupling: a general control strategy
for transporting objects. J Exp Psychol Hum Percept Perform. 1994 Oct; 20(5):944-57.
Flanagan, J. R. and Wing, A. M. (1993) Modulation of grip force with load force during
point-to-point arm movements. Exp Brain Res . 1993; 95(1):131-43.
Flanagan, J. R. and Wing, A. M. (1995) The stability of precision grip forces during cyclic
arm movements with a hand-held load. Exp Brain Res . 1995; 105(3):455-64.
Flanagan JR and Johansson RS. (2002) Hand movements. Ramshandran VS, ed. Encyclopaedia
of the human brain . San Diego: Academic Press; 2002; pp. 399-414.
Fu JL, Pollard NS (2006) On the importance of asymmetries in grasp quality metrics for
tendon driven hands. IEEE/RSJ International Conference on Intelligent Robots and
Systems (IROS) ; Beijing, China. Beijing; 2006: 1068-1075.
Gao F, Latash ML, and Zatsiorsky V M (2004) Neural network modeling supports a theory
on the hierarchical control of prehension. Neural Computing & Applications. 2004;
13(4): 352-359.
Gao F, Latash ML, and Zatsiorsky VM (2005a) Control of finger force direction in the
flexion-extension plane. Exp Brain Res . 2005 Mar; 161(3):307-15.
Gao F, Latash ML, and Zatsiorsky VM (2005b) Internal forces during object manipulation.
Exp Brain Res . 2005 Aug; 165(1):69-83.
464
Parallel Manipulators, Towards New Applications
Gao F, Latash ML Zatsiorsky VM. (2005c) In contrast to robots, in humans internal and
manipulation forces are coupled (ThP01-18 ). Proceedings of the 2005 IEEE 9th
International Conference on Rehabilitation Robotics ; Chicago, IL, USA. 2005: 404-407.
Gao F, Li S, Li ZM, Latash ML, and Zatsiorsky VM. (2003) Matrix analyses of interaction
among fingers in static force production tasks. Biol Cybern . 2003 Dec; 89(6):407-14.
Gordon AM, Charles J, and Duff SV (1999) Fingertip forces during object manipulation in
children with hemiplegic cerebral palsy. II: bilateral coordination. Dev Med Child
Neurol . 1999 Mar; 41(3):176-85.
Gysin P, Kaminski TR, and Gordon, A. M. (2003) Coordination of fingertip forces in object
transport during locomotion. Exp Brain Res . 2003 Apr; 149(3):371-9.
Iberall T (1987) The nature of human prehension: Three dexterous hands in one. Proc. 1987
IEEE Int. Conf. on Robotics and Automation ; Raleigh, NC. 1987; 396-401.
Johansson, R. S. and Westling, G. (1984) Roles of glabrous skin receptors and sensorimotor
memory in automatic control of precision grip when lifting rougher or more
slippery objects. Exp Brain Res . 1984; 56(3):550-64.
Kerr JR, Roth B. (1986) Analysis of multifingered hands. Journal of Robotics Research . 1986;
4(4):3-17.
Kilbreath, S. L.; Gorman, R. B.; Raymond, J., and Gandevia, S. C. (2002) Distribution of the
forces produced by motor unit activity in the human flexor digitorum profundus. J
Physiol . 2002 Aug 15; 543(Pt 1):289-96.
Kilbreath SL and Gandevia SC. (1994) Limited independent flexion of the thumb and fingers
in human subjects. J Physiol . 1994; 479 (Pt 3):487-97.
Kinoshita H; Kawai S; Ikuta K , and Teraoka T. (1996) Individual finger forces acting on a
grasped object during shaking actions. Ergonomics . 1996; 39(2):243-56; ISSN: 0014-
0139.
Latash Ml; Gao F, and Zatsiorsky VM. (2003) Similarities and differences in finger
interaction across typical and atypical populations. Journal of Applied Biomechanics .
2003; 19(3):264-270.
Li ZM; Latash ML , and Zatsiorsky VM. Force sharing among fingers as a model of the
redundancy problem. Exp Brain Res . 1998a; 119(3):276-86.
Li ZM; Latash ML; Newell KM, and Zatsiorsky VM. (1998b) Motor redundancy during
maximal voluntary contraction in four-finger tasks. Exp Brain Res . 1998; 122(1):71-7.
Li ZM; Zatsiorsky VM; Latash ML; Bose NK. (2002) Anatomically and experimentally based
neural networks modeling force coordination in static mult-finger tasks.
Neurocomputing . 2002; 47:259-275.
MacKenzie CL and Iberall T. (1994) The grasping hand . Amsterdam; New York: North-
Holland.; 1994.
Mason MT and Salisbury JK. (1985) Robot Hands and the Mechanics of Manipulation .
Cambridge, MS: The MIT Press; 1985.
Murray RM; Li Z, and Sastry SS. (1994) A Mathematical Introduction to Robotic Manipulation .
Roca Baton, FL: CRC Press; 1994.
Nakazawa, N.; Ikeura, R., and Inooka, H. (2000) Characteristics of human fingertips in the
shearing direction. Biol Cybern. 2000 Mar; 8(3):207-14.
Nakazawa N; Uekita Y; Inooka H, and Ikeura R. (1996) Experimental study on human
grasping force. IEEE International Workshop on Robot and Human Communication .
1996; pp. 280-285.
Human Hand as a Parallel Manipulator
465
Niu, X.; Latash, M. L., and Zatsiorsky, V. M. (2007) Prehension synergies in the grasps with
complex friction patterns: local versus synergic effects and the template control. J
Neurophysiol. 2007 Jul; 98(1):16-28.
Pare, M. and Dugas, C. (1999) Developmental changes in prehension during childhood. Exp
Brain Res . 1999 Apr; 125. 125(3. 3):239-47.
Pataky, T. C.; Latash, M. L., and Zatsiorsky, V. M. (2005) Viscoelastic response of the finger
pad to incremental tangential displacements. J Biomech . 2005 Jul; 38(7):1441-9.
Schieber, M. H. and Santello, M. (2004) Hand function: peripheral and central constraints on
performance. J Appl Physiol . 2004 Jun; 96(6):2293-300.
Serina, E. R. and Rempel, D. M. (1996) Fingertip pulp response during keystrikes. Twentieth
Annual Meeting of the American Society of Biomechanics, Conference Proceedings ;
Georgia Tech, Atlanta, Georgia. 1996: 237-238.
Shim, J. K.; Latash, M. L., and Zatsiorsky, V. M. (2005a) Prehension synergies in three
dimensions. J Neurophysiol. 2005 Feb; 93(2): 766-76.
Shim, J. K.; Latash, M. L., and Zatsiorsky, V. M. (2005b) Prehension synergies: trial-to-trial
variability and principle of superposition during static prehension in three
dimensions. J Neurophysiol . 2005 Jun; 93(6):3649-58.
Shim, J. K. and Park, J. (2007) Prehension synergies: principle of superposition and
hierarchical organization in circular object prehension. Exp Brain Res. 2007 Jul;
180(3):541-56.
Smith, M. A. and Soechting, J. F. (2005) Modulation of grasping forces during object
transport. J Neurophysiol. 2005 Jan; 93(1):137-45.
Srinivasan, M. A. (1989) Surface deflection of primate fingertip under line load. J Biomech .
1989; 22(4):343-9.
Srinivasan, M. A; Gulati, R. J., and Dandekar, K. (1992) In vivo compressibility of the
human fingertip. Advances in Bioengineering, Proceedings of the ASME (Ed. M.W.
Bidez). 1992; 22:573-576.
Yoshikawa T and Nagai K. (1980) Analysis of multi-fingered grasping and manipulation.
Venkarataman ST and Iberall T, eds. Dextrous Robot Hands . New York: Springer-
Verlag; 1990; pp. 187-208.
Yoshikawa T and Nagai K. (1991) Manipulating and grasping forces in manipulation by
multifingered robot hands. IEEE Trans Robot. Autom . 1991; 7:67-77.
Zatsiorsky, V. M.; Gao, F., and Latash, M. L. (2003) Finger force vectors in multi-finger
prehension. J Biomech. 2003 Nov; 36(11):1745-9.
Zatsiorsky, V. M.; Gao, F., and Latash, M. (2006) Prehension stability: experiments with
expanding and contracting handle. J Neurophysiol. 2006 Apr; 95(4):2513-29.
Zatsiorsky, V. M.; Gregory, R. W., and Latash, M. L. (2002a) Force and torque production in
static multifinger prehension: biomechanics and control. I. Biomechanics. Biol
Cybern. 2002a; 87(1):50-7.
Zatsiorsky, V. M.; Gregory, R. W., and Latash, M. L. (2002b) Force and torque production in
static multifinger prehension: biomechanics and control. II. Control. Biol Cybern.
2002b; 87(1):40-9.
Zatsiorsky, V. M. and Latash, M. L. (2004) Prehension synergies. Exerc Sport Sci Rev. 2004
Apr; 32(2):75-80.
Zatsiorsky, V. M.; Li, Z. M., and Latash, M. L. (2000) Enslaving effects in multi-finger force
production. Exp Brain Res . 2000 Mar; 131(2):187-95.
466
Parallel Manipulators, Towards New Applications
Zatsiorsky VM and Latash ML. (2008) Multi-finger prehension: An Overview. Journal of
Motor Behavior . 2008; (In press.).
Zatsiorsky VM; Latash ML; Danion F; Gao F; Li ZM; Gregory RW, and Li S. (2004a) Inter-
finger connection matricesBubak M; van Albada GD; Sloot PMA, and Dongarra JJ,
Eds. Computational Science - ICCS 2004, 4th International Conference ; Krakow, Poland.
Berlin: Springer; 2004: 1056-1064.
Zatsiorsky VM; Latash ML; Gao F, and Shim JK. (2004b) The principle of superposition in
human prehension. Robotica. 2004; 22:231-234.
Zatsiorsky VM; Li ZM, and Latash ML. (1998) Coordinated force production in multi-finger
tasks: finger interaction and neural network modeling. Biol Cybern. 1998 Aug;
79(2):139-50; ISSN: 0340-1200.
Zuo, B. R. and Qian, W. H. (2000) A general dynamic force distribution algorithm for
multifingered grasping. IEEE Transactions on Systems Man and Cybernetics Part B-
Cybernetics . 2000 Feb; 30(1):185-192.
!"#
$%&'(')*#%+#,-.)'.(#/.0.((1(#$.2'-3(.)%04#
Jing-Shan *hao, Fulei Chu and *hi-Jing Feng
Department of Precision Instruments and Mechanology,
Tsinghua University, Beijing 100084,
P. R. China.
"5#62)0%738)'%2#
This chapter focuses on the mobility analysis of spatial parallel manipulators. It first
develops an analytical methodology to investigate the instantaneous degree of freedom
(DOF) of the end-effector of a parallel manipulator. And then, the instantaneous
controllability of the end-effector is discussed from the viewpoint of the possible actuation
schemes which will be especially useful for the designers of the parallel manipulators. Via
comparing the differences and essential mobility of a set of underactuated, over actuated
and equally actuated manipulators, this chapter demonstrates that the underactuated, over
actuated and equally actuated manipulators are all substantially fully actuated mechanisms.
This work is significantly important for a designer to contrive his or her manipulators with
underactuated or over actuated structures.
Based on the analytical model of the DOF of a spatia ! $ "
!
#$ # 0
(16)
)! 3 I 3&
where $ !
$ # # '
$ , and I 3 and ! 3 are 3* 3 identity and
(I 3 ! 3%
zero matrices, respectively.
Similarly, if one gets a set of terminal constraints exerted to a rigid body, its free motion(s)
can also be solved through equation (16). Next, one can investigate the instantaneous
mobility of the end-effector of a parallel manipulator with equation (16).
!5"5#9:1#71;011#%+#+0117%<#%+#):1#127=1++18)%0#%+#.#-.0.((1(#<.2'-3(.)%0#
The free motions of the end-effector can be instantaneously expressed in a set of PlPcker
homogeneous coordinates in one Cartesian coordinate system. The main steps are:
!"#$%&'()*+,)'#)-'#.'/0*%,1#23%()/,*%)(#34#)-'#5*%'0,)*6#2-,*%(#
In general, any parallel manipulator can be decomposed into $ ! $ + "
1 kinematic chains
connecting the end effector with the base. In order to instantaneously analyze the mobility
properties of the end-effector, this section only establishes one absolute coordinate system.
After establishing the coordinate system, the Pl$cker homogeneous coordinates of all
kinematic pairs in a chain can be obtained. Group all of the kinematic screws of the same
chain to be %
$ % # ,
1 2 , , $r
$ %
468
Parallel Manipulators, Towards New Applications
In fact, if all of the terminal constraints of the kinematic chains are gained, the constraints
exerted to the end-effector, denoted by '
$ #
constraint spaces spanned by the terminal constraints of kinematic chains can be simplified
as
1
) #
'
R'$( $ # ,.
/
.
0
-
7"#831&'#)-'#9/''#:3)*3%;(<=# (
$ # =#34#)-'#>%?@>44'6)3/#A*)-#>BC,)*3%#;!D<#
Naturally, the mobility properties of the end-effector is fully expressed by (
$ #
DOF can be expressed as:
(
*
R'$( 1
#
$
/
# 6 )
#
2
(17)
0
-
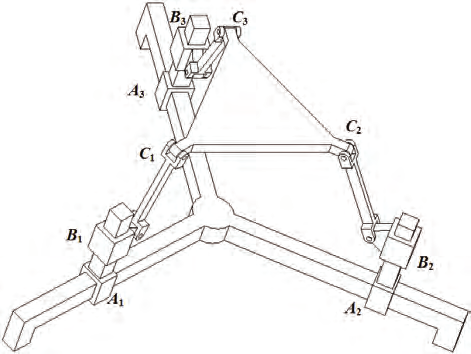
Now, the DOF of the end-effector of the parallel manipulator shown in Fig. 1 can be
instantaneously investigated with the above two steps. In this manipulator, the end-effector
1
+ + 2 3
+ has three identical PPRR kinematic chains connected with the fixed base. For the
sake of modelling, one can establish any Cartesian coordinate system for the manipulator.
Assume that the direction vector of the prismatic joint , ! % # 1, 2,3 is denoted by
%
"
/, # ! '% 1
%
.
-
1
" "
%
, the direction vector of the prismatic joint 0 ! % # 1, 2,3 is denoted by
%
"
%
1
/0 # ! '% 2
%
.
-
2
" "
%
, the rotational vector of the revolute joint
%
2
%
0 is denoted by
/ #
*
#
2
2
2
, the rotational vector of the revolute joint
!
/
/
. -
. -
' -
' -
' .
' .
0
,
0
! % 1 % 2 % 2 % 1 % 2 % 1 % 1 % 2 % 1 % 2
Page 1 Page 2 Page 3 Page 4 Page 5 Page 6 Page 7 Page 8 Page 9 Page 10 Page 11 Page 12 Page 13 Page 14 Page 15 Page 16 Page 17 Page 18 Page 19 Page 20 Page 21 Page 22 Page 23 Page 24 Page 25 Page 26 Page 27 Page 28 Page 29 Page 30 Page 31 Page 32 Page 33 Page 34 Page 35 Page 36 Page 37 Page 38 Page 39 Page 40 Page 41 Page 42 Page 43