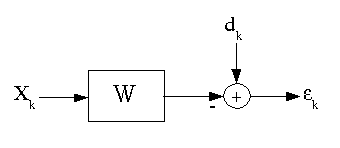
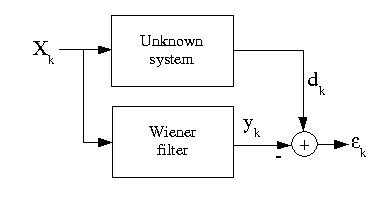
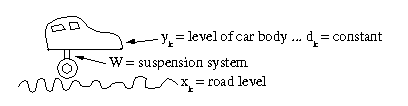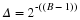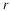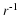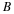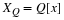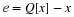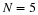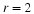Quadratic minimization problems
The least squares optimal filter design problem is quadratic
in the filter coefficients:
E[ε2]=rdd(0)−2PTW+WTRW
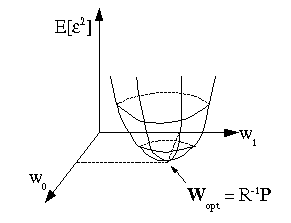
If R is positive definite, the
error surface
E[ε2](w0, w1, …, wM
–
1
)
is a unimodal "bowl" in
ℝN.
The problem is to find the bottom of the bowl. In an
adaptive filter context, the shape and bottom of the bowl may
drift slowly with time; hopefully slow enough that the
adaptive algorithm can track it.
For a quadratic error surface, the bottom of the bowl can be
found in one step by computing
R-1P
. Most modern nonlinear optimization methods (which
are used, for example, to solve the
LP optimal IIR filter design problem!) locally
approximate a nonlinear function with a second-order
(quadratic) Taylor series approximation and step to the bottom
of this quadratic approximation on each iteration. However, an
older and simpler appraoch to nonlinear optimaztion exists,
based on gradient descent.
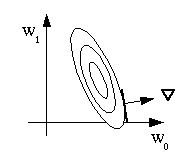
The idea is to iteratively find the minimizer by computing
the gradient of the error function:
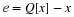 . The gradient is a vector in
ℝM pointing in the steepest uphill direction on the
error surface at a given point
Wi, with ∇ having a
magnitude proportional to the slope of the error surface in
this steepest direction.
. The gradient is a vector in
ℝM pointing in the steepest uphill direction on the
error surface at a given point
Wi, with ∇ having a
magnitude proportional to the slope of the error surface in
this steepest direction.
By updating the coefficient vector by taking a step
opposite the gradient direction :
Wi+1=Wi−μ∇i, we go (locally) "downhill" in the steepest
direction, which seems to be a sensible way to iteratively
solve a nonlinear optimization problem. The performance
obviously depends on μ; if
μ is too large, the
iterations could bounce back and forth up out of the
bowl. However, if μ is too
small, it could take many iterations to approach the
bottom. We will determine criteria for choosing
μ later.
In summary, the gradient descent algorithm for solving the
Weiner filter problem is:
Guess
W0
do
i=1
,
∞
∇i=–(2P)+2R