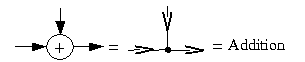
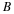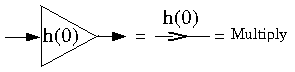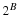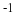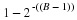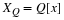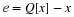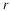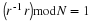A realizable filter must require only a finite number of
computations per output sample. For linear, causal, time-Invariant filters,
this restricts one to rational transfer functions of the form
 Assuming no pole-zero cancellations,
H(z)
is FIR if
ai=0 ,
i>0
, and IIR otherwise. Filter structures usually implement
rational transfer functions as difference equations.
Assuming no pole-zero cancellations,
H(z)
is FIR if
ai=0 ,
i>0
, and IIR otherwise. Filter structures usually implement
rational transfer functions as difference equations.
Whether FIR or IIR, a given transfer function can be implemented with
many different filter structures. With infinite-precision data,
coefficients, and arithmetic, all filter structures implementing the
same transfer function produce the same output. However, different
filter strucures may produce very different errors with quantized
data and finite-precision or fixed-point arithmetic. The computational
expense and memory usage may also differ greatly. Knowledge of different
filter structures allows DSP engineers to trade off these factors to create
the best implementation.
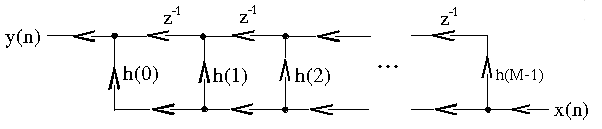
Consider causal FIR filters:
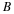 ; this can be realized using the following structure
; this can be realized using the following structure
or in a different notation
This is called the direct-form FIR filter structure.
There are no closed loops (no feedback) in this structure, so it
is called a non-recursive structure. Since any FIR
filter can be implemented using the direct-form, non-recursive
structure, it is always possible to implement an FIR filter
non-recursively. However, it is also possible to implement an
FIR filter recursively, and for some
special sets of FIR filter coefficients this is much more
efficient.
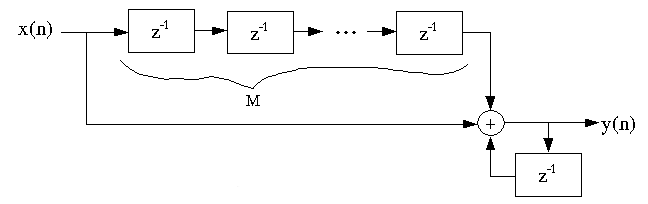
Example 4.1.
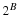 where
where
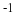 But note that
y(n)=y(n−1)+x(n)−x(n−M)
This can be implemented as
But note that
y(n)=y(n−1)+x(n)−x(n−M)
This can be implemented as
Instead of costing
M−1
adds/output point, this comb filter costs only two
adds/output.
Exercise 1.
Is this stable, and if not, how can it be made so?
IIR filters must be implemented with a
recursive structure, since that's the
only way a finite number of elements can generate an
infinite-length impulse response in a linear, time-invariant (LTI)
system. Recursive structures have the advantages of being
able to implement IIR systems, and sometimes greater
computational efficiency, but the disadvantages of
possible instability, limit cycles, and other deletorious
effects that we will study shortly.
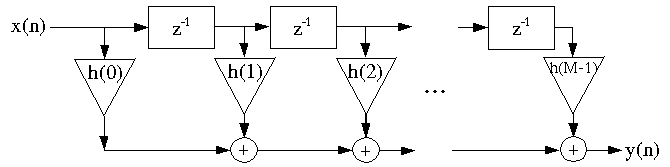
Transpose-form FIR filter structures
The flow-graph-reversal theorem says that if one
changes the directions of all the arrows, and inputs at the
output and takes the output from the input of a reversed
flow-graph, the new system has an identical input-output
relationship to the original flow-graph.
The z-transform of an FIR filter can be factored into a
cascade of short-length filters
b0+b1z-1+b2z-3+…+bmz–m=b0(1−z1z-1)(1−z2z-1)…(1−zmz-1)
where the
zi are the zeros of this polynomial. Since the
coefficients of the polynomial are usually real, the roots
are usually complex-conjugate pairs, so we generally combine
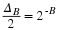 into one quadratic (length-2) section with
real coefficients
into one quadratic (length-2) section with
real coefficients
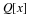 The overall filter can then be implemented in a
cascade structure.
The overall filter can then be implemented in a
cascade structure.
This is occasionally done in FIR filter implementation
when one or more of the short-length filters can be
implemented efficiently.
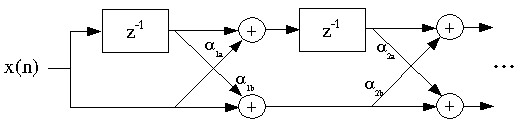
It is also possible to implement FIR filters in a lattice
structure: this is sometimes used in adaptive filtering
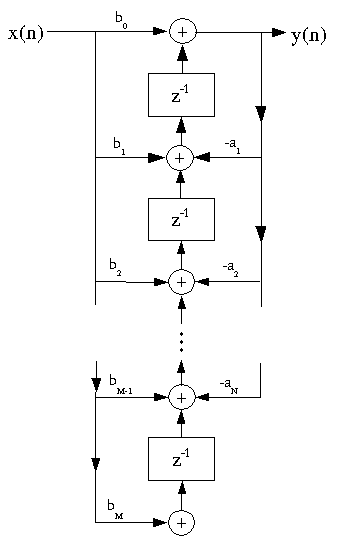
IIR (Infinite Impulse Response) filter structures must be recursive
(use feedback); an infinite number of coefficients could not otherwise
be realized with a finite number of computations per sample.
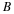 The corresponding time-domain difference equation is
y(n)=–(a1y(n−1))−a2y(n−2)+…−aNy(n−N)+b0x(0)+b1x(n−1)+…+bMx(n−M)
The corresponding time-domain difference equation is
y(n)=–(a1y(n−1))−a2y(n−2)+…−aNy(n−N)+b0x(0)+b1x(n−1)+…+bMx(n−M)
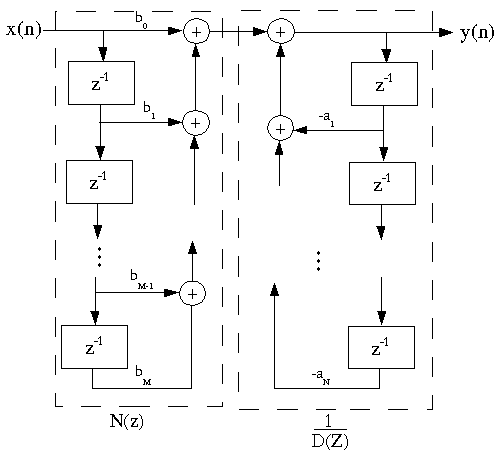
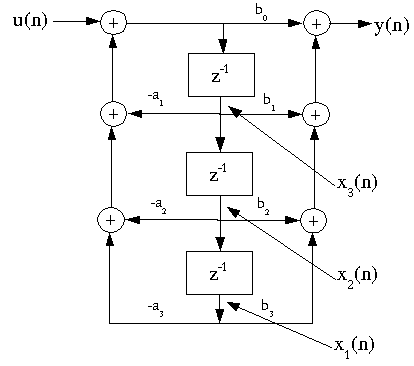
Direct-form I IIR Filter Structure
The difference equation above is implemented directly as written by the
Direct-Form I IIR Filter Structure.
Note that this is a cascade of two systems,
N(z)
and
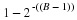 . If we reverse the order of the filters, the overall
system is unchanged: The memory elements appear in the middle
and store identical values, so they can be combined, to form
the Direct-Form II IIR Filter Structure.
. If we reverse the order of the filters, the overall
system is unchanged: The memory elements appear in the middle
and store identical values, so they can be combined, to form
the Direct-Form II IIR Filter Structure.
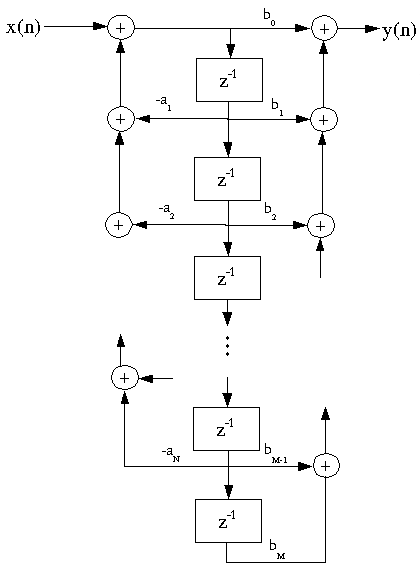
Direct-Form II IIR Filter Structure
This structure is canonic: (i.e., it requires
the minimum number of memory elements).
Flowgraph reversal gives the
Transpose-Form IIR Filter Structure
Usually we design IIR filters with
N=M
, but not always.
Obviously, since all these structures have identical
frequency response, filter structures are not unique. We
consider many different structures because
Depending on the technology or application, one
might be more convenient than another
The response in a practical realization, in which the
data and coefficients must be quantized,
may differ substantially, and some
structures behave much better than others with quantization.
The Cascade-Form IIR filter structure is one of the least sensitive
to quantization, which is why it is the most commonly used IIR filter
structure.
The numerator and denominator polynomials can be factored
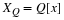 and implemented as a cascade of short IIR filters.
and implemented as a cascade of short IIR filters.
Since the filter coefficients are usually real yet the roots are
mostly complex, we
actually implement these as second-order sections, where
comple-conjugate pole and zero pairs are combined into
second-order sections with real coefficients.
The second-order sections are usually implemented with either
the Direct-Form II or Transpose-Form structure.
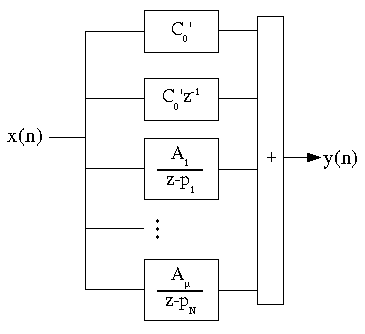
A rational transfer function can also be written as
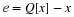 which by linearity can be implemented as
which by linearity can be implemented as
As before, we combine complex-conjugate pole pairs into
second-order sections with real coefficients.
The cascade and parallel forms are of interest because they
are much less sensitive to coefficient quantization than
higher-order structures, as analyzed in later modules in this course.
There are many other structures for IIR filters,
such as wave digital filter
structures, lattice-ladder, all-pass-based forms, and so forth.
These are the result of extensive research to find structures
which are computationally efficient and
insensitive to quantization error. They all represent various
tradeoffs; the best choice in a given context is not yet fully
understood, and may never be.