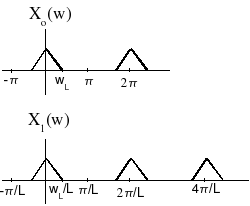
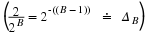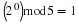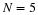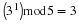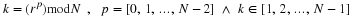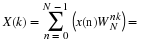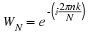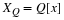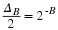Restrictions on h(n) to get linear phase
()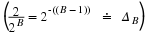
For linear phase, we require the right side of Equation to be
ⅇ–(ⅈθ0)(real,positive function of ω)
. For
θ0=0
, we thus require
h(0)+h(M−1)=real number
h(0)−h(M−1)=pure imaginary number
h(1)+h(M−2)=pure real number
h(1)−h(M−2)=pure imaginary number
⋮
Thus
h(k)=h*(M−1−k)
is a necessary condition for
the right side of Equation to be real valued, for
θ0=0
.
For
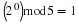 , or
ⅇ–(ⅈθ0)=–ⅈ
, we require
h(0)+h(M−1)=pure imaginary
h(0)−h(M−1)=pure real number
⋮
⇒
h(k)=–(h*(M−1−k))
, or
ⅇ–(ⅈθ0)=–ⅈ
, we require
h(0)+h(M−1)=pure imaginary
h(0)−h(M−1)=pure real number
⋮
⇒
h(k)=–(h*(M−1−k))
Usually, one is interested in filters with
real-valued coefficients, or see Figure 3.2 and Figure 3.3.
Filter design techniques are usually slightly different for
each of these four different filter types. We will study the
most common case, symmetric-odd length, in detail, and often
leave the others for homework or tests or for when one
encounters them in practice. Even-symmetric filters are often
used; the anti-symmetric filters are rarely used in practice,
except for special classes of filters, like differentiators or
Hilbert transformers, in which the desired response is
anti-symmetric.
So far, we have satisfied the condition that
 where
A(ω)
is real-valued. However, we have
not assured that
A(ω)
is non-negative. In general,
this makes the design techniques much more difficult, so most
FIR filter design methods actually design filters with
Generalized Linear Phase:
where
A(ω)
is real-valued. However, we have
not assured that
A(ω)
is non-negative. In general,
this makes the design techniques much more difficult, so most
FIR filter design methods actually design filters with
Generalized Linear Phase:
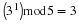 , where
A(ω)
is real-valued, but possible negative.
A(ω)
is called the amplitude of the frequency
response.
, where
A(ω)
is real-valued, but possible negative.
A(ω)
is called the amplitude of the frequency
response.
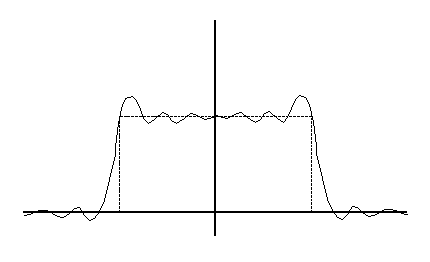
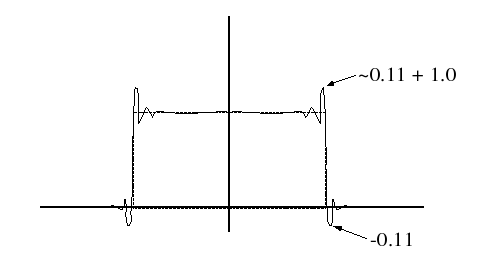
Example 3.1.
Lowpass Filter
Time-delay introduces generalized linear phase.
For odd-length FIR filters, a linear-phase design
procedure is equivalent to a zero-phase design procedure
followed by an
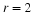 -sample delay of the impulse response. For
even-length filters, the delay is non-integer, and the
linear phase must be incorporated directly in the desired
response!
-sample delay of the impulse response. For
even-length filters, the delay is non-integer, and the
linear phase must be incorporated directly in the desired
response!