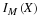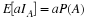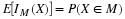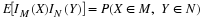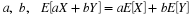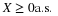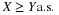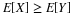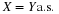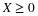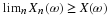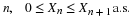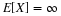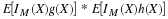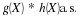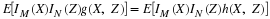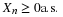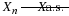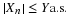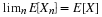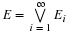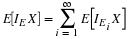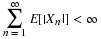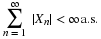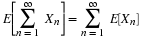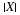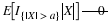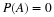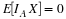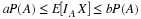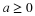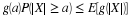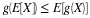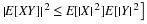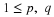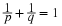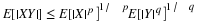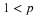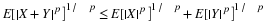Expectation for simple random variables
The notion of mathematical expectation is closely related to the idea of a weighted mean, used
extensively in the handling of numerical data. Consider the arithmetic average  of the following ten numbers: 1, 2, 2, 2, 4, 5, 5, 8, 8, 8, which is given by
of the following ten numbers: 1, 2, 2, 2, 4, 5, 5, 8, 8, 8, which is given by
Examination of the ten numbers to be added shows that five distinct values are included. One of
the ten, or the fraction 1/10 of them, has the value 1, three of the ten, or the fraction 3/10 of them,
have the value 2, 1/10 has the value 4, 2/10 have the value 5, and 3/10 have the value 8. Thus, we
could write
The pattern in this last expression can be stated in words: Multiply each possible value by the fraction of the numbers having that value and then sum these
products. The fractions are often referred to as the relative frequencies. A sum of this
sort is known as a weighted average.
In general, suppose there are n numbers 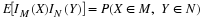 to be averaged, with
m≤n distinct values
to be averaged, with
m≤n distinct values
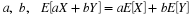 . Suppose f1 have value t1,
f2 have value
. Suppose f1 have value t1,
f2 have value 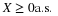 have value tm. The fi must add to n. If we
set pi=fi/n, then the fraction pi is called the relative frequency of those numbers in the
set which have the value ti,1≤i≤m. The average
have value tm. The fi must add to n. If we
set pi=fi/n, then the fraction pi is called the relative frequency of those numbers in the
set which have the value ti,1≤i≤m. The average 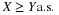 of the n numbers
may be written
of the n numbers
may be written
In probability theory, we have a similar averaging process in which the relative frequencies of
the various possible values of are replaced by the probabilities that those values are observed on
any trial.
Definition. For a simple random variable X with values 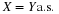 and corresponding probabilities
and corresponding probabilities 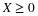 , the mathematical expectation, designated
E[X], is the probability weighted average of the values taken on by X. In symbols
, the mathematical expectation, designated
E[X], is the probability weighted average of the values taken on by X. In symbols
Note that the expectation is determined by the distribution. Two quite different random
variables may have the same distribution, hence the same expectation.
Traditionally, this average has been called the mean, or the mean value, of
the random variable X.
Example 11.1. Some special cases
Since X=aIE=0IEc+aIE, we have 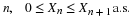 .
.
For X a constant c, X=cIΩ, so that E[c]=cP(Ω)=c.
If 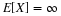 then
then  ,
so that
,
so that
Mechanical interpretation
In order to aid in visualizing an essentially abstract
system, we have employed the notion of probability as mass. The distribution induced by
a real random variable on the line is visualized as a unit of probability mass actually
distributed along the line. We utilize the mass distribution to give an important and
helpful mechanical interpretation of the expectation or mean value. In Example 6 in "Mathematical Expectation: General Random Variables",
we give an alternate interpretation in terms of mean-square estimation.
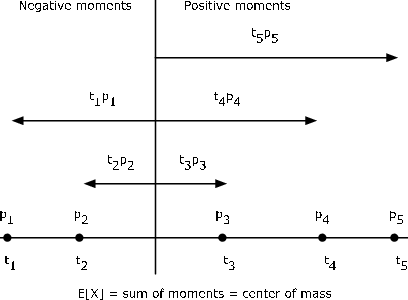
Suppose the random variable X has values 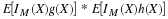 , with
, with 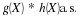 . This produces a probability mass distribution, as shown in Figure 1, with point mass concentration
in the amount of pi at the point ti. The expectation is
. This produces a probability mass distribution, as shown in Figure 1, with point mass concentration
in the amount of pi at the point ti. The expectation is
Now |ti| is the distance of point mass pi from the origin, with pi to the left of the
origin iff ti is negative. Mechanically, the sum of the products tipi is the moment
of the probability mass distribution about the origin on the real line. From physical theory, this
moment is known to be the same as the product of the total mass times the number which locates
the center of mass. Since the total mass is one, the mean value is the
location of the center of mass. If the real line is viewed as a stiff, weightless
rod with point mass pi attached at each value ti of X, then the mean value μX is the
point of balance. Often there are symmetries in the distribution which make it possible to
determine the expectation without detailed calculation.
Example 11.2. The number of spots on a die
Let X be the number of spots which turn up on a throw of a simple six-sided die. We
suppose each number is equally likely. Thus the values are the integers one through six,
and each probability is 1/6. By definition
Although the calculation is very simple in this case, it is really not necessary.
The probability distribution places equal mass at each of the integer values one through
six. The center of mass is at the midpoint.
Example 11.3. A simple choice
A child is told she may have one of four toys. The prices are $2.50. $3.00, $2.00, and
$3.50, respectively. She choses one, with respective probabilities 0.2, 0.3, 0.2, and 0.3 of choosing the first,
second, third or fourth. What is the expected cost of her selection?
(11.8)
E
[
X
]
=
2
.
00
·
0
.
2
+
2
.
50
·
0
.
2
+
3
.
00
·
0
.
3
+
3
.
50
·
0
.
3
=
2
.
85
For a simple random variable, the mathematical expectation is
determined as the dot product of the value matrix with the probability matrix. This is easily
calculated using MATLAB.
Example 11.4. MATLAB calculation for Example 3
X = [2 2.5 3 3.5]; % Matrix of values (ordered)
PX = 0.1*[2 2 3 3]; % Matrix of probabilities
EX = dot(X,PX) % The usual MATLAB operation
EX = 2.8500
Ex = sum(X.*PX) % An alternate calculation
Ex = 2.8500
ex = X*PX' % Another alternate
ex = 2.8500
Expectation and primitive form
The definition and treatment above assumes X is in canonical form, in which case
We wish to ease this restriction to canonical form.
Suppose simple random variable X is in a primitive form
We show that
Before a formal verification, we begin with an example which exhibits the essential pattern.
Establishing the general case is simply a matter of appropriate use of notation.
Example 11.5. Simple random variable X in primitive form
Inspection shows the distinct possible values of X to be 1, 2, or 3. Also,
so that
Now
To establish the general pattern, consider 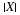 .
We identify the distinct set of values contained
in the set
.
We identify the distinct set of values contained
in the set 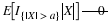 . Suppose these are t1<t2<⋯<tn.
For any value ti in the range, identify the index set Ji of those j such
that cj=ti. Then the terms
. Suppose these are t1<t2<⋯<tn.
For any value ti in the range, identify the index set Ji of those j such
that cj=ti. Then the terms
By the additivity of probability
Since for each j∈Ji we have cj=ti, we have
— □
Thus, the defining expression for expectation thus holds for X in a primitive form.
An alternate approach to obtaining the expectation from a primitive form is to use the csort
operation to determine the distribution of X from the coefficients and probabilities of
the primitive form.
Example 11.6. Alternate determinations of E[X]
Suppose X in a primitive form is
(11.20)
X
=
IC1
+
2
IC2
+
IC3
+
3
IC4
+
2
IC5
+
2
IC6
+
IC7
+
3
IC8
+
2
IC9
+
IC10
with respective probabilities
c = [1 2 1 3 2 2 1 3 2 1]; % Matrix of coefficients
pc = 0.01*[8 11 6 13 5 8 12 7 14 16]; % Matrix of probabilities
EX = c*pc'
EX = 1.7800 % Direct solution
[X,PX] = csort(c,pc); % Determination of dbn for X
disp([X;PX]')
1.0000 0.4200
2.0000 0.3800
3.0000 0.2000
Ex = X*PX' % E[X] from distribution
Ex = 1.7800
Linearity
The result on primitive forms may be used to establish the linearity of mathematical
expectation for simple random variables. Because of its fundamental importance, we work through
the verification in some detail.
Suppose 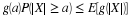 and
and 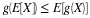 (both in canonical form). Since
(both in canonical form). Since
we have
Note that IAiIBj=IAiBj and 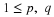 . The
class of these sets for all possible pairs
. The
class of these sets for all possible pairs 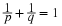 forms a partition. Thus, the last
summation expresses Z=X+Y in a primitive form. Because of the result on primitive forms, above, we have
forms a partition. Thus, the last
summation expresses Z=X+Y in a primitive form. Because of the result on primitive forms, above, we have
We note that for each i and for each j
Hence, we may write