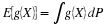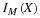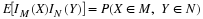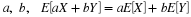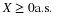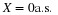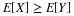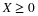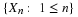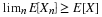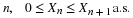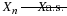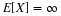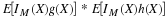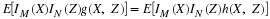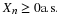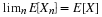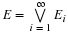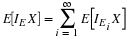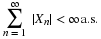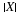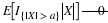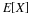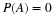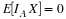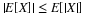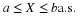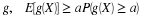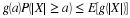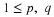The usual treatments deal with a single random variable or a fixed, finite number of random variables, considered jointly. However, there are many common applications in which we select at random a member of a class of random variables and observe its value, or select a random number of random variables and obtain some function of those selected. This is formulated with the aid of a counting or selecting random variable N, which is nonegative, integer valued. It may be independent of the class selected, or may be related in some sequential way to members of the class. We consider only the independent case. Many important problems require optional random variables, sometimes called Markov times. These involve more theory than we develop in this treatment.

Some common examples:

As a basic model, we consider the sum of a random number of members of an iid class. In order to have a concrete interpretation to help visualize the formal patterns, we think of the demand of a random number of customers. We suppose the number of customers N is independent of the individual demands. We formulate a model to be used for a variety of applications.

Note. In some applications the counting random variable may take on the idealized value ∞. For example, in a game that is played until some specified result occurs, this may never happen, so that no finite value can be assigned to N. In such a case, it is necessary to decide what value X_∞ is to be assigned. For N independent of the Y_n (hence of the X_n), we rarely need to consider this possibility.

Independent selection from an iid incremental sequence

We assume throughout, unless specifically stated otherwise, that:

We utilize repeatedly two important propositions:

DERIVATION

We utilize properties of generating functions, moment generating functions, and conditional expectation.

— □

Remark. The result on M_D and g_D may be developed without use of conditional expectation.

(15.5)

(15.6)

— □

Example 15.1.  A service shop

Suppose the number N of jobs brought to a service shop in a day is Poisson (8). One fourth of these are items under warranty for which no charge is made. Others fall in one of two categories. One half of the arriving jobs are charged for one hour of shop time; the remaining one fourth are charged for two hours of shop time. Thus, the individual shop hour charges Y_k have the common distribution

(15.7)

Make the basic assumptions of our model. Determine P(D≤4).

SOLUTION

(15.8)

According to the formula developed above,

(15.9)

Expand the exponentials in power series about the origin, multiply out to get enough terms. The result of straightforward but somewhat tedious calculations is

(15.10)

Taking the coefficients of the generating function, we get

(15.11)

Example 15.2.  A result on Bernoulli trials

Suppose the counting random variable N∼ binomial and Y_i=I_Ei, with . Then

(15.12)

By the basic result on random selection, we have

(15.13)

so that D∼ binomial .

In the next section we establish useful m-procedures for determining the generating function g_D and the moment generating function M_D for the compound demand for simple random variables, hence for determining the complete distribution. Obviously, these will not work for all problems. It may helpful, if not entirely sufficient, in such cases to be able to determine the mean value E[D] and variance . To this end, we establish the following expressions for the mean and variance.

Example 15.3. Mean and variance of the compound demand

(15.14)

DERIVATION

(15.15)

(15.16)

(15.17)

(15.18)

Hence

(15.19)

Example 15.4. Mean and variance for Example 15.1

. By symmetry E[Y]=1. . Hence,

(15.20)

We have m-procedures for performing the calculations necessary to determine the distribution for a composite demand D when the counting random variable N and the individual demands Y_k are simple random variables with not too many values. In some cases, such as for a Poisson counting random variable, we are able to approximate by a simple random variable.

The procedure gend

If the Y_i are nonnegative, integer valued, then so is D, and there is a generating function. We examine a strategy for computation which is implemented in the m-procedure gend. Suppose

The coefficients of g_N and g_Y are the probabilities of the values of N and Y, respectively. We enter these and calculate the coefficients for powers of g_Y:

(15.23)

We wish to generate a matrix P whose rows contain the joint probabilities. The probabilities in the ith row consist of the coefficients for the appropriate power of g_Y multiplied by the probability N has that value. To achieve this, we need a matrix, each of whose n+1 rows has nm+1 elements, the length of yn. We begin by “preallocating” zeros to the rows. That is, we set P=zeros(n+1,n*m+1). We then replace the appropriate elements of the successive rows. The replacement probabilities for the ith row are obtained by the convolution of g_Y and the power of g_Y for the previous row. When the matrix P is completed, we remove zero rows and columns, corresponding to missing values of N and D (i.e., values with zero probability). To orient the joint probabilities as on the plane, we rotate P ninety degrees counterclockwise. With the joint distribution, we may then calculate any desired quantities.

gN = (1/3)*[0 1 1 1];    % Note zero coefficient for missing zero power
gY = 0.1*[5 4 1];        % All powers 0 thru 2 have positive coefficients
gend
 Do not forget zero coefficients for missing powers
Enter the gen fn COEFFICIENTS for gN gN    % Coefficient matrix named gN
Enter the gen fn COEFFICIENTS for gY gY    % Coefficient matrix named gY
Results are in N, PN, Y, PY, D, PD, P
May use jcalc or jcalcf on N, D, P
To view distribution for D, call for gD
disp(gD)                  % Optional display of complete distribution
         0    0.2917
    1.0000    0.3667
    2.0000    0.2250
    3.0000    0.0880
    4.0000    0.0243
    5.0000    0.0040
    6.0000    0.0003
EN = N*PN'
EN =   2
EY = Y*PY'
EY =  0.6000
ED = D*PD'
ED =  1.2000                % Agrees with theoretical EN*EY
P3 = (D>=3)*PD'
P3  = 0.1167                
[N,D,t,u,PN,PD,PL] = jcalcf(N,D,P);
EDn = sum(u.*P)./sum(P);
disp([N;EDn]')
    1.0000    0.6000        % Agrees with theoretical E[D|N=n] = n*EY
    2.0000    1.2000
    3.0000    1.8000
VD = (D.^2)*PD' - ED^2
VD =  1.1200                % Agrees with theoretical EN*VY + VN*EY^2

Example 15.6. A numerical example

(15.24)

Note that the zero power is missing from gY, corresponding to the fact that P(Y=0)=0.

gN = 0.2*[1 1 1 1 1];
gY = 0.1*[0 5 3 2];      % Note the zero coefficient in the zero position
gend
Do not forget zero coefficients for missing powers
Enter the gen fn COEFFICIENTS for gN  gN
Enter the gen fn COEFFICIENTS for gY  gY
Results are in N, PN, Y, PY, D, PD, P
May use jcalc or jcalcf on N, D, P
To view distribution for D, call for gD
disp(gD)                 % Optional display of complete distribution
         0    0.2000
    1.0000    0.1000
    2.0000    0.1100
    3.0000    0.1250
    4.0000    0.1155
    5.0000    0.1110
    6.0000    0.0964
    7.0000    0.0696
    8.0000    0.0424
    9.0000    0.0203
   10.0000    0.0075
   11.0000    0.0019
   12.0000    0.0003

p3 = (D == 3)*PD'        % P(D=3)
P3 =  0.1250
P4_12 = ((D >= 4)&(D <= 12))*PD'
P4_12 = 0.4650           % P(4 <= D <= 12)