168 Chapter 3
We now have a quadratic equation for revenue as a function of the subscription charge.
To find the price that will maximize revenue for the newspaper, we can find the vertex:
000
,
159
h = −
=
8
.
31
2(−
)
500
,
2
The model tells us that the maximum revenue will occur if the newspaper charges
$31.80 for a subscription. To find what the maximum revenue is, we can evaluate the
revenue equation:
Maximum Revenue = −
.
31
(
500
,
2
)
8 2 +
,
159
)
8
.
31
(
000
= $2,528,100
Short run Behavior: Intercepts
As with any function, we can find the vertical intercepts of a quadratic by evaluating the
function at an input of zero, and we can find the horizontal intercepts by solving for when
the output will be zero. Notice that depending upon the location of the graph, we might
have zero, one, or two horizontal intercepts.
zero horizontal intercepts one horizontal intercept two horizontal intercepts
Example 6
Find the vertical and horizontal intercepts of the quadratic f ( x) = 3 2
x + 5 x − 2
We can find the vertical intercept by evaluating the function at an input of zero:
f ( )
0 = (
3 0)2 + (
5 )
0 − 2 = 2
−
Vertical intercept at (0,-2)
For the horizontal intercepts, we solve for when the output will be zero
0 = 3 2
x + 5 x − 2
In this case, the quadratic can be factored easily, providing the simplest method for
solution
0 = 3
( x − )(
1 x + )
2
0 = 3 x −1
0 = x + 2
1
1
or
Horizontal intercepts at 0
, and (-2,0)
x =
x = 2
−
3
3
3.2 Quadratic Functions 169
Notice that in the standard form of a quadratic, the constant term c reveals the vertical
intercept of the graph.
Example 7
Find the horizontal intercepts of the quadratic f ( x) = 2 2
x + 4 x − 4
Again we will solve for when the output will be zero
0 = 2 2
x + 4 x − 4
Since the quadratic is not easily factorable in this case, we solve for the intercepts by
first rewriting the quadratic into transformation form.
b
4
h = −
= −
= 1
−
k = f (− )
1 = 2(− )
1 2 + (
4 − )
1 − 4 = 6
−
2 a
(
2 )
2
f ( x) = (
2 x + )
1 2 − 6
Now we can solve for when the output will be zero
0 = (
2 x + )
1 2 − 6
6 = (
2 x + )
1 2
3 = ( x + )
1 2
x +1 = ± 3
x = 1
− ± 3
The graph has horizontal intercepts at ( 1
− − 3, )
0 and ( 1
− + 3 0
, )
Try it Now
3. In Try it Now problem 2 we found the standard & transformation form for the
function g( x) = 13 + x 2 − 6 x . Now find the Vertical & Horizontal intercepts (if any).
This process is done commonly enough that sometimes people find it easier to solve the
problem once in general and remember the formula for the result, rather than repeating
the process each time. Based on our previous work we showed that any quadratic in
standard form can be written into transformation form as:
b 2
b 2
f ( x) = a x +
+ c −
2 a
4 a
170 Chapter 3
Solving for the horizontal intercepts using this general equation gives:
b 2
b 2
0 = a x +
+ c −
start to solve for x by moving the constants to the other side
2 a
4 a
2
2
b
b
− c = a x +
divide both sides by a
4 a
2 a
2
2
b
c
b
− = x +
find a common denominator to combine fractions
2
4 a
a
2 a
2
2
b
4 ac
b
−
= x +
combine the fractions on the left side of the equation
2
2
4 a
4 a
2 a
2
2
b − 4 ac
b
= x +
take the square root of both sides
2
4 a
2 a
b 2 − 4 ac
b
±
= x +
subtract b/2 a from both sides
4 a 2
2 a
b
b 2 − 4 ac
−
±
= x
combining the fractions
2 a
2 a
− b ± b 2 − 4 ac
x =
Notice that this can yield two different answers for x
2 a
Quadratic Formula
For a quadratic function given in standard form
2
f ( x) = ax + bx + c , the quadratic
formula gives the horizontal intercepts of the graph of this function.
− b ± b 2 − 4 ac
x =
2 a
Example 8
A ball is thrown upwards from the top of a 40 foot high building at a speed of 80 feet
per second. The ball’s height above ground can be modeled by the equation
2
H ( t) = 16
− t + 80 t + 40 .
What is the maximum height of the ball?
When does the ball hit the ground?
To find the maximum height of the ball, we would need to know the vertex of the
quadratic.
80
80 5
2
h = −
=
= ,
5
5
5
k H
16
80
=
= −
+
+ 40 =
140
(
2 16
− ) 32 2
2
2
2
The ball reaches a maximum height of 140 feet after 2.5 seconds.
3.2 Quadratic Functions 171
To find when the ball hits the ground, we need to determine when the height is zero –
when H(t) = 0. While we could do this using the transformation form of the quadratic,
we can also use the quadratic formula:
− 80 ± 802 − (
4 − )(
16
)
40
− 80 ± 8960
t =
=
(
2 − )
16
− 32
Since the square root does not simplify nicely, we can use a calculator to approximate
the values of the solutions:
− 80 − 8960
t
−
+
=
≈ 458
.
5
or
80
8960
t =
≈ − 458
.
0
− 32
− 32
The second answer is outside the reasonable domain of our model, so we conclude the
ball will hit the ground after about 5.458 seconds.
Try it Now
4. For these two equations determine if the vertex will be a maximum value or a
minimum value.
a. g( x) = 8
2
− x + x + 7
b. g( x) = − 3
(
3 − x)2 + 2
Important Topics of this Section
Quadratic functions
Standard form
Transformation form/Vertex form
Vertex as a maximum / Vertex as a minimum
Short run behavior
Vertex / Horizontal & Vertical intercepts
Quadratic formula
Try it Now Answers
1. The path passes through the origin with vertex at (-4, 7).
7
2
h( x) = − ( x + 4) + 7 . To make the shot, h(-7.5) would
16
need to be about 4. h( 7.5
−
) ≈1.64; he doesn’t make it.
2. g( x)
2
= x − 6 x +13 in Standard form; g( x) = ( x − )
3 2 + 4 in Transformation form
3. Vertical intercept at (0, 13), NO horizontal intercepts.
4. a. Vertex is a minimum value
b. Vertex is a maximum value
172 Chapter 3
Section 3.2 Exercises
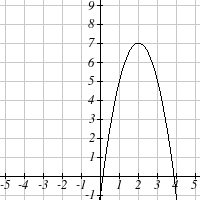
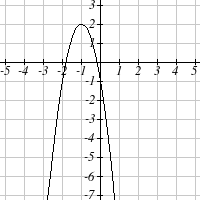
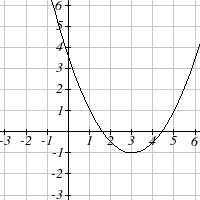
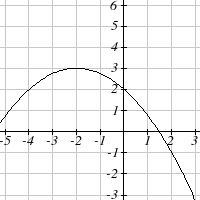
Write an equation for the quadratic function graphed.
1.
2.
3.
4.
5.
6.
For each of the follow quadratic functions, find a) the vertex, b) the vertical intercept, and
c) the horizontal intercepts.
7. y ( x)
2
= 2 x +10 x +12
8. z ( p)
2
= 3 x + 6 x − 9
9. f ( x)
2
= 2 x −10 x + 4
10. g ( x)
2
= 2
− x −14 x +12
11. h( t)
2
= 4
− t + 6 t −1
12. k ( t)
2
= 2 x + 4 x −15
Rewrite the quadratic function into vertex form.
13. f ( x)
2
= x −12 x + 32
14. g ( x)
2
= x + 2 x − 3
15. h( x)
2
= 2 x + 8 x −10
16. k ( x)
2
= 3 x − 6 x − 9
3.2 Quadratic Functions 173
17. Find the values of b and c so f ( x)
2
= 8
− x + bx + c has vertex (2, 7
− )
18. Find the values of b and c so f ( x)
2
= 6 x + bx + c has vertex (7, 9)
−
Write an equation for a quadratic with the given features
19. x-intercepts (-3, 0) and (1, 0), and y intercept (0, 2)
20. x-intercepts (2, 0) and (-5, 0), and y intercept (0, 3)
21. x-intercepts (2, 0) and (5, 0), and y intercept (0, 6)
22. x-intercepts (1, 0) and (3, 0), and y intercept (0, 4)
23. Vertex at (4, 0), and y intercept (0, -4)
24. Vertex at (5, 6), and y intercept (0, -1)
25. Vertex at (-3, 2), and passing through (3, -2)
26. Vertex at (1, -3), and passing through (-2, 3)
27. A rocket is launched in the air. Its height, in meters above sea level, as a function of
time, in seconds, is given by h( t)
2
= 4.9
−
t + 229 t + 234 .
a. From what height was the rocket launched?
b. How high above sea level does the rocket reach its peak?
c. Assuming the rocket will splash down in the ocean, at what time does
splashdown occur?
28. A ball is thrown in the air from the top of a building. Its height, in meters above
ground, as a function of time, in seconds, is given by h( t)
2
= 4.9
−
t + 24 t + 8.
a. From what height was the ball thrown?
b. How high above ground does the ball reach its peak?
c. When does the ball hit the ground?
29. The height of a ball thrown in the air is given by h( x)
1 2
= −
x + 6 x + 3, where x is
12
the horizontal distance in feet from the point at which the ball is thrown.
a. How high is the ball when it was thrown?
b. What is the maximum height of the ball?
c. How far from the thrower does the ball strike the ground?
30. A javelin is thrown in the air. Its height is given by h( x)
1 2
= −
x + 8 x + 6 , where x
20
is the horizontal distance in feet from the point at which the javelin is thrown.
a. How high is the javelin when it was thrown?
b. What is the maximum height of the javelin?
c. How far from the thrower does the javelin strike the ground?
174 Chapter 3
31. A box with a square base and no top is to be made from a square piece of cardboard
by cutting 6 in. squares out of each corner and folding up the sides. The box needs to
hold 1000 in3. How big a piece of cardboard is needed?
32. A box with a square base and no top is to be made from a square piece of cardboard
by cutting 4 in. squares out of each corner and folding up the sides. The box needs to
hold 2700 in3. How big a piece of cardboard is needed?
33. A farmer wishes to enclose two pens with fencing, as shown.
If the farmer has 500 feet of fencing to work with, what
dimensions will maximize the area enclosed?
34. A farmer wishes to enclose three pens with fencing, as shown.
If the farmer has 700 feet of fencing to work with, what
dimensions will maximize the area enclosed?
35. You have a wire that is 56 cm long. You wish to cut it into two pieces. One piece will
be bent into the shape of a square. The other piece will be bent into the shape of a
circle. Let A represent the total area enclosed by the square and the circle. What is the
circumference of the circle when A is a minimum?
36. You have a wire that is 71 cm long. You wish to cut it into two pieces. One piece will
be bent into the shape of a right triangle with legs of equal length. The other piece
will be bent into the shape of a circle. Let A represent the total area enclosed by the
triangle and the circle. What is the circumference of the circle when A is a minimum?
37. A soccer stadium holds 62,000 spectators. With a ticket price of $11, the average
attendance has been 26,000. When the price dropped to $9, the average attendance
rose to 31,000. Assuming that attendance is linearly related to ticket price, what ticket
price would maximize revenue?
38. A farmer finds that if she plants 75 trees per acre, each tree will yield 20 bushels of
fruit. She estimates that for each additional tree planted per acre, the yield of each tree
will decrease by 3 bushels. How many trees should she plant per acre to maximize her
harvest?
3.2 Quadratic Functions 175
39. A hot air balloon takes off from the
edge of a mountain lake. Impose a
coordinate system as pictured and
assume that the path of the balloon
follows the graph of
f ( x)
2
2
= −
x + 45 x . The land rises
2500
at a constant incline from the lake at the
rate of 2 vertical feet for each 20
horizontal feet. [UW]
a. What is the maximum height of the balloon above water level?
b. What is the maximum height of the balloon above ground level?
c. Where does the balloon land on the ground?
d. Where is the balloon 50 feet above the ground?
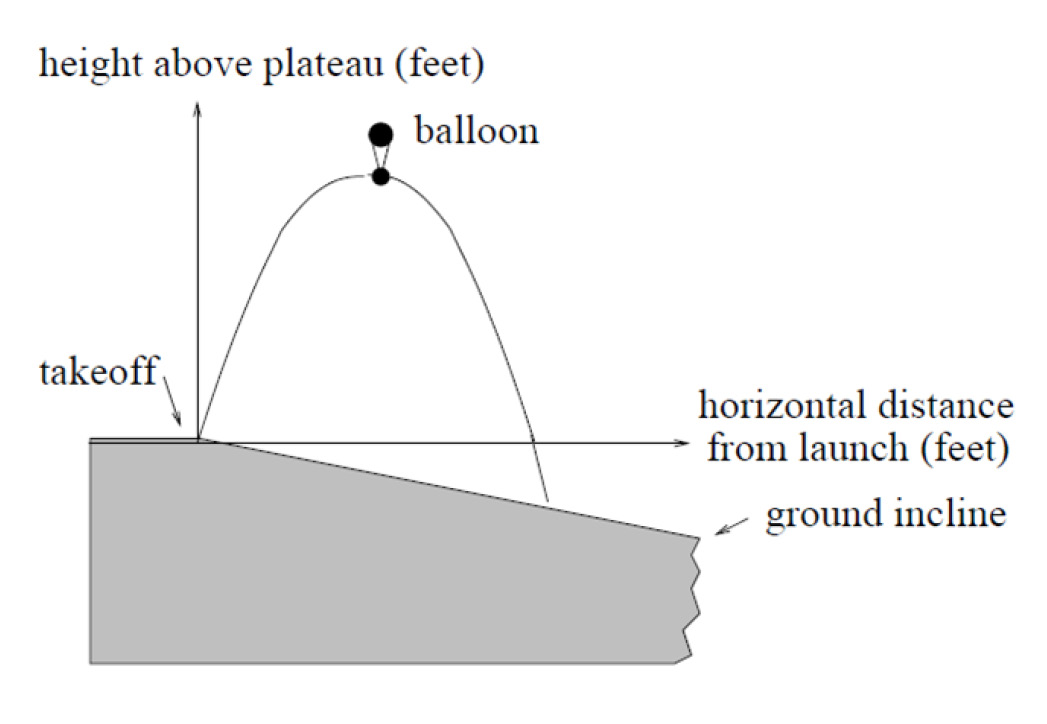
40. A hot air balloon takes off from
the edge of a plateau. Impose a
coordinate system as pictured
below and assume that the path
the balloon follows is the graph
of the quadratic function
f ( x)
4
2
4
= −
x + x . The
2500
5
land drops at a constant incline
from the plateau at the rate of 1
vertical foot for each 5