From the transformation form of the function, we can see this is a transformed quadratic
with vertex at (2,-3) that opens upwards. Since the graph will be decreasing on one
side of the vertex, and increasing on the other side, we can restrict this function to a
domain on which it will be one-to-one by limiting the domain to x ≥ 2.
To find the inverse, we will use the vertex form of the quadratic. We start by replacing
the f(x) with a simple variable y, then solve for x.
y = ( x − 2)2 − 3
Add 3 to both sides
2
y + 3 = ( x − )
2
Take the square root
± y + 3 = x − 2
Add 2 to both sides
2 ± y + 3 = x
208 Chapter 3
Of course, as written this is not a function. Since we restricted our original function to a
domain of x ≥ 2, the outputs of the inverse should be the same, telling us to utilize the
+ case:
1
x = −
f ( y) = 2 + y + 3
If the quadratic had not been given in vertex form, rewriting it into vertex form is
probably the best approach. Alternatively, we could have taken the standard equation
and rewritten it equal to zero:
0 = x 2 − 4 x + 1 − y
We would then be able to use the quadratic formula with a =1, b= 4−, and c=(1− y), resulting in the same solutions we found above:
2
−( 4)
− ± ( 4)
−
− 4(1)(1− y)
12 + 4 y
x =
= 2 ±
= 2 ± 3+ y
2
2
Try it Now
1. Find the inverse of the function
2
f ( x) = x +1, on the domain x ≥ 0 .
While it is not possible to find an inverse of most polynomial functions, some other basic
polynomials are invertible.
Example 3
Find the inverse of the function f ( x) = 5 3
x +1.
This is a transformation of the basic cubic toolkit function, and based on our knowledge
of that function, we know it is one-to-one. Solving for the inverse by solving for x
3
y = 5 x +1
3
y −1 = 5 x
y −1
3
= x
5
1
−
y −1
x = f
y = 3
( )
5
Notice that this inverse is also a transformation of a power function with a fractional
power, x 1/3.
Try it Now
2. Which toolkit functions have inverse functions without restricting their domain?
3.5 Inverses and Radical Functions 209
Besides being important as an inverse function, radical functions are common in
important physical models.
Example 4
The velocity, v in feet per second, of a car that slammed on its brakes can be determined
based on the length of skid marks that the tires left on the ground. This relationship is
given by
v( d) = 2 gfd
In this formula, g represents acceleration due to gravity (32 ft/sec2), d is the length of
the skid marks in feet, and f is a constant representing the friction of the surface. A car
lost control on wet asphalt, with a friction coefficient of 0.5, leaving 200 foot skid
marks. How fast was the car travelling when it lost control?
Using the given values of f = 0.5 and d = 200, we can evaluate the given formula:
v(200) = 2(32)(0.5)(200) = 80 ft/sec , which is about 54.5 miles per hour.
When radical functions are composed with other functions, determining domain can
become more complicated.
Example 5
x +
x −
Find the domain of the function
(
)(
2
)
3
f ( x) =
.
( x − )
1
Since a square root is only defined when the quantity under the radical is non-negative,
x +
x −
we need to determine where (
)(
2
)
3 ≥ 0. A rational function can change signs
( x − )
1
(change from positive to negative or vice versa) at horizontal intercepts and at vertical
asymptotes. For this equation, the graph could change signs at x = -2, 1, and 3.
To determine on which intervals the rational expression is positive, we could evaluate
the expression at test values, or sketch a graph. While both approaches work equally
well, for this example we will use a graph.
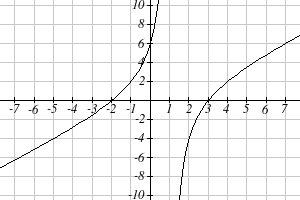
This function has two horizontal intercepts, both of which exhibit linear behavior,
where the graph will pass through the intercept. There is one vertical asymptote,
corresponding to a linear factor, leading to a behavior similar to the basic reciprocal
toolkit function. There is a vertical intercept at (0, 6). This graph does not have a
horizontal asymptote, since the degree of the numerator is larger than the degree of the
denominator.
210 Chapter 3
From the vertical intercept and horizontal intercept at x = -2, we can sketch the left side
of the graph. From the behavior at the asymptote, we can sketch the right side of the
graph.
From the graph, we can now tell on which
intervals this expression will be non-negative,
so the original function f(x) will be defined.
f(x) has domain − 2 ≤ x < 1 or x ≥ 3, or in
interval notation, [− )
1
,
2 ∪ ,
3
[ ∞) .
Like with finding inverses of quadratic functions, it is sometimes desirable to find the
inverse of a rational function, particularly of rational functions that are the ratio of linear
functions, such as our concentration examples.
Example 6
20 +
The function
.
0 4 n
C( n) =
was used in the previous section to represent the
100 + n
concentration of an acid solution after n mL of 40% solution has been added to 100 mL
of a 20% solution. We might want to be able to determine instead how much 40%
solution has been added based on the current concentration of the mixture.
To do this, we would want the inverse of this function:
20 + 0 4
. n
C =
multiply both sides by the denominator
100 + n
C 100
(
+ n) = 20 + 4
.
0 n
distribute
C
100 + Cn = 20 + 0 4
. n
group everything with n on one side
C
100 − 20 = 4
.
0 n − Cn
factor out n
C
100 − 20 = ( 4
.
0 − C) n
divide to find the inverse
C
n C
100 −
( ) =
20
0 4
. − C
If, for example, we wanted to know how many mL of 40% solution need to be added to
obtain a concentration of 35%, we can simply evaluate the inverse rather than solving
an equation involving the original function:
100(0 )
35
.
− 20
15
n(
)
35
.
0
=
=
= 300mL of 40% solution would need to be added.
.
0 4 − 35
.
0
.
0 05
Try it Now
+
3. Find the inverse of the function
x 3
f ( x) =
.
x − 2
3.5 Inverses and Radical Functions 211
Important Topics of this Section
Imposing a coordinate system
Finding an inverse function
Restricting the domain
Invertible toolkit functions
Radical Functions
Inverses of rational functions
Try it Now Answers
1.
1
x = −
f ( y) = y −1
2. identity, cubic, square root, cube root
+
3. 1−
2 y 3
f ( y) =
y −1
212 Chapter 3
Section 3.5 Exercises
For each function, find a domain on which the function is one-to-one and non-decreasing,
then find an inverse of the function on this domain.
1. f ( x) = ( x − )2
4
2. f ( x) = ( x + )2
2
3. f ( x)
2
= 12 − x
4. f ( x)
2
= 9 − x
5. f ( x)
3
= 3 x +1
6. f ( x)
3
= 4 − 2 x
Find the inverse of each function.
7. f ( x) = 9 + 4 x − 4
8. f ( x) = 6 x −8 + 5
9. f ( x)
3
= 9 + 2 x
10. f ( x)
3
= 3− x
11. f ( x)
2
=
12. f ( x)
3
=
x + 8
x − 4
+
−
13. f ( x) x 3
=
14. f ( x) x 2
=
x + 7
x + 7
+
+
15. f ( x) 3 x 4
=
16. f ( x) 5 x 1
=
5 − 4 x
2 − 5 x
Police use the formula v = 20 L to estimate the speed of a car, v, in miles per hour, based on the length, L, in feet, of its skid marks when suddenly braking on a dry, asphalt
road.
17. At the scene of an accident, a police officer measures a car's skid marks to be 215 feet
long. Approximately how fast was the car traveling?
18. At the scene of an accident, a police officer measures a car's skid marks to be 135 feet
long. Approximately how fast was the car traveling?
The formula v = 2.7 r models the maximum safe speed, v, in miles per hour, at which a car can travel on a curved road with radius of curvature r, in feet.
19. A highway crew measures the radius of curvature at an exit ramp on a highway as
430 feet. What is the maximum safe speed?
20. A highway crew measures the radius of curvature at a tight corner on a highway as
900 feet. What is the maximum safe speed?
3.5 Inverses and Radical Functions 213
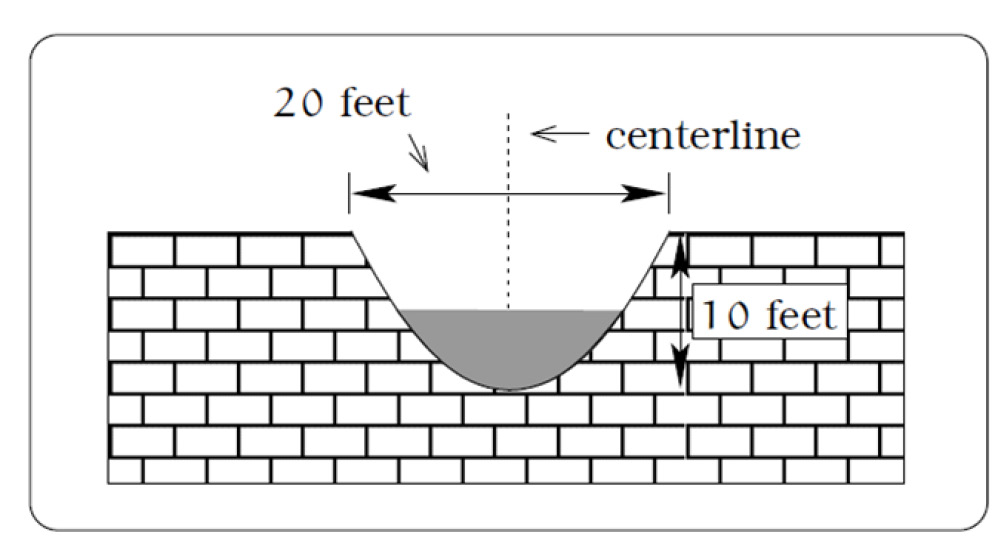
21. A drainage canal has a cross-
section in the shape of a parabola.
Suppose that the canal is 10 feet
deep and 20 feet wide at the top. If
the water depth in the ditch is 5
feet, how wide is the surface of the
water in the ditch? [UW]
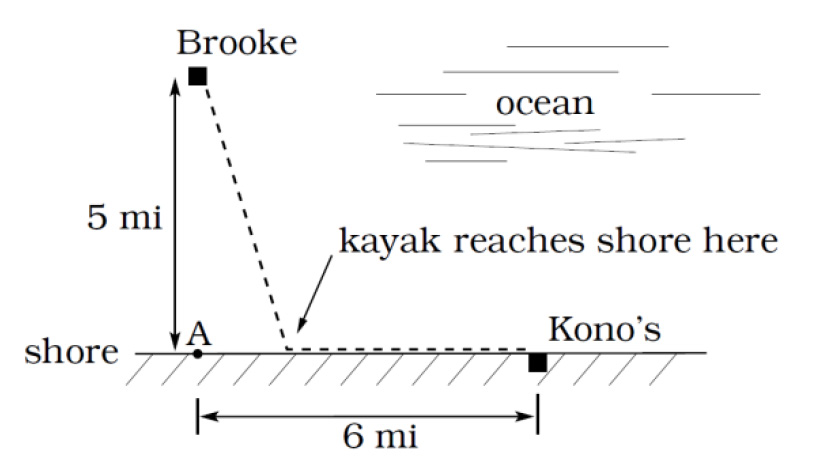
22. Brooke is located 5 miles out from the
nearest point A along a straight shoreline in
her sea kayak. Hunger strikes and she wants
to make it to Kono’s for lunch; see picture.
Brooke can paddle 2 mph and walk 4 mph.
[UW]
a. If she paddles along a straight line
course to the shore, find an
expression that computes the total time to reach lunch in terms of the location
where Brooke beaches her kayak.
b. Determine the total time to reach Kono’s if she paddles directly to the point A.
c. Determine the total time to reach Kono’s if she paddles directly to Kono’s.
d. Do you think your answer to b or c is the minimum time required for Brooke
to reach lunch?
e. Determine the total time to reach Kono’s if she paddles directly to a point on
the shore half way between point A and Kono’s. How does this time compare
to the times in parts b or c? Do you need to modify your answer to part d?
23. Clovis is standing at the edge of a dropoff, which slopes 4 feet downward from him
for every 1 horizontal foot. He launches a small model rocket from where he is
standing. With the origin of the coordinate system located where he is standing, and
the x-axis extending horizontally, the path of the rocket is described by the formula
2
y = 2
− x +120 x . [UW]
a. Give a function h = f ( x) relating the height h of the rocket above the sloping ground to its x-coordinate.
b. Find the maximum height of the rocket above the sloping ground. What is its
x-coordinate when it is at its maximum height?
c. Clovis measures the height h of the rocket above the sloping ground while it is
going up. Give a function x = g ( h) relating the x-coordinate of the rocket to h.
d. Does the function from (c) still work when the rocket is going down? Explain.
214 Chapter 3
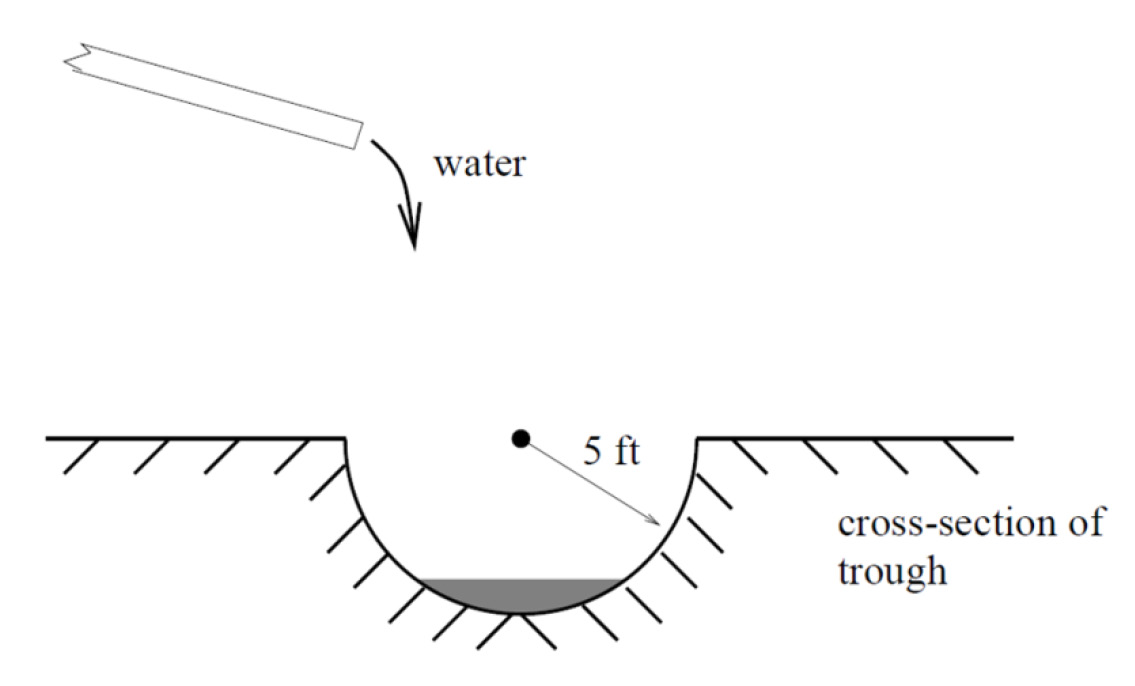
24. A trough has a semicircular
cross section with a radius
of 5 feet. Water starts
flowing into the trough in
such a way that the depth of
the water is increasing at a
rate of 2 inches per hour.
[UW]
a. Give a function
w = f ( t) relating
the width w of the surface of the water to the time t, in hours. Make sure to
specify the domain and compute the range too.
b. After how many hours will the surface of the water have width of 6 feet?
c. Give a function
1
t f −
=
( w) relating the time to the width of the surface of the
water. Make sure to specify the domain and compute the range too.
Chapter 4: Exponential and Logarithmic Functions
Section 4.1 Exponential Functions
India is the second most populous country in the world, with a population in 2008 of
about 1.14 billion people. The population is growing by about 1.34% each year1. We might ask if we can find a formula to model the population, P, as a function of time, t, in years after 2008, if the population continues to grow at this rate.
In linear growth, we had a constant rate of change – a constant number that the output
increased for each increase in input. For example, in the equation f ( x) = 3 x + 4 , the slope tells us the output increases by three each time the input increases by one. This
population scenario is different – we have a percent rate of change rather than a constant
number of people as our rate of change. To see the significance of this difference
consider these two companies:
Company A has 100 stores, and expands by opening 50 new stores a year
Company B has 100 stores, and expands by increasing the number of stores by 50% of
their total each year.
Looking at a few years of growth for these companies:
Year Stores, company A
Stores, company B
0
100
Starting with 100 each 100
1
100 + 50 = 150
They both grow by 50
100 + 50% of 100
stores in the first year.
100 + 0.50(100) = 150
2
150 + 50 = 200
Store A grows by 50,
150 + 50% of 150
Store B grows by 75
150 + 0.50(150) = 225
3
200 + 50 = 250
Store A grows by 50,
225 + 50% of 225
Store B grows by 112.5 225 + 0.50(225) = 337.5
1 World Bank, World Development Indicators, as reported on http://www.google.com/publicdata, retrieved August 20, 2010
This chapter is part of Precalculus: An Investigation of Functions © Lippman & Rasmussen 2011.
This material is licensed under a Creative Commons CC-BY-SA license.
216 Chapter 4
Notice that with the percent growth, each year the company is grows by 50% of the
current year’s total, so as the company grows larger, the number of stores added in a year
grows as well.
To try to simplify the calculations, notice that after 1 year the number of stores for
company B was:
100 +
)
100
(
50
.
0
or equivalently by factoring
1
(
100 +
)
50
.
0
= 150
We can think of this as “the new number of stores is the original 100% plus another
50%”.
After 2 years, the number of stores was:
150 +
)
150
(
50
.
0
or equivalently by factoring
1
(
150 + .
0 )
50
now recall the 150 came from 100(1+0.50). Substituting that,
1
(
100 +
1
)(
50
.
0
+ .
0 )
50 =
1
(
100 +
)
50
.
0
2 = 225
After 3 years, the number of stores was:
225 +
(
50
.
0
)
225
or equivalently by factoring
1
(
225 +
)
50
.
0
now recall the 225 came from