2
g( x) = (
increasing and decreasing?
x − ) + 3
1 2
This is a transformation of the toolkit reciprocal squared function,
1
f ( x) =
:
2
x
2
− 2 f
−
( x) =
A vertical flip and vertical stretch by 2
2
x
− 2
− 2 f ( x − )
1 = (
A shift right by 1
x − )2
1
− 2
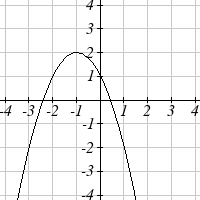
− 2 f ( x − )
1 + 3 = (
A shift up by 3
x − ) + 3
1 2
The basic reciprocal squared function is increasing on
(−∞ )
0
, and decreasing on ( ,
0 ∞) . Because of the vertical
flip, the g(x) function will be decreasing on the left and
increasing on the right. The horizontal shift right by 1 will
also shift these intervals to the right one. From this, we can
determine g(x) will be increasing on ,1
( ∞) and decreasing on
(−∞ )
1
, . We also could graph the transformation to help us
determine these intervals.
Try it Now
6. On what interval(s) is the function h( t) = ( t − )
3 3 + 2 concave up and down?
Section 1.5 Transformation of Functions 81
Important Topics of This Section
Transformations
Vertical Shift (up & down)
Horizontal Shifts (left & right)
Reflections over the vertical & horizontal axis
Even & Odd functions
Vertical Stretches & Compressions
Horizontal Stretches & Compressions
Combinations of Transformation
Try it Now Answers
1.
2
b( t) = h( t) +10 = 4.9
−
t + 30 t +10
2. a. Horizontal shift
b. The function is shifted to the LEFT by 2 units.
c. Shown to the right
3. Shown to the right
Notice: g(x) = f(-x) looks the same as f(x)
4.
1
g( x) = f x so using the square root function we get
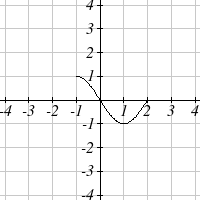
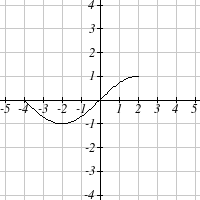
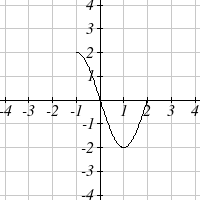
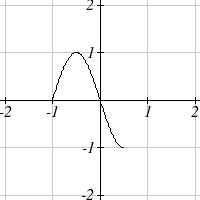
3
1
g( x) =
x
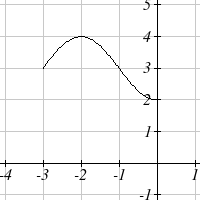
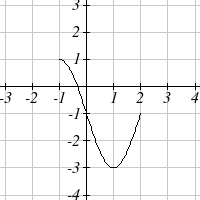
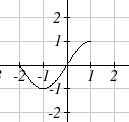
3
5. The identity tool kit function f(x) = x has been
transformed in 3 steps
a. Vertically stretched by 2.
b. Vertically reflected over the x axis.
c. Vertically shifted up by 1 unit.
6. h(t) is concave down on (−∞ )3,and concave up on ,3(∞)
82 Chapter 1
Section 1.5 Exercises
Describe how each function is a transformation of the original function f( x)
1. f ( x − 49)
2. f ( x + 43)
3. f ( x + 3)
4. f ( x − 4)
5. f ( x) + 5
6. f ( x) + 8
7. f ( x) − 2
8. f ( x) − 7
9. f ( x − 2) + 3
10. f ( x + 4) −1
11. Write a formula for f ( x) = x shifted up 1 unit and left 2 units.
12. Write a formula for f ( x) = x shifted down 3 units and right 1 unit.
13. Write a formula for
1
f ( x) = shifted down 4 units and right 3 units.
x
14. Write a formula for
1
f ( x) =
shifted up 2 units and left 4 units.
2
x
15. Tables of values for f ( x) , g( x) , and h( x) are given below. Write g( x) and h( x) as transformations of f ( x) .
x -2 -1 0 1 2
x -1 0 1 2 3
x -2 -1 0 1 2
h(x) -1 0 -2 2 3
g(x) -2 -1 -3 1 2
f(x) -2 -1 -3 1 2
16. Tables of values for f ( x) , g( x) , and h( x) are given below. Write g( x) and h( x) as transformations of f ( x) .
x -2 -1 0 1 2
x -3 -2 -1 0 1
x -2 -1 0 1 2
h(x) -2 -4 3 1 0
g(x) -1 -3 4 2 1
f(x) -1 -3 4 2 1
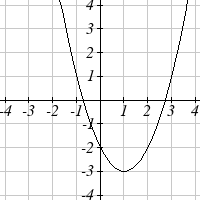
The graph of ( ) 2 x
f x = is shown. Sketch a graph of each transformation of f ( x)
17. ( ) 2 x
g x = +1
18. ( ) 2 x
h x = − 3
19. ( )
1
2 x
w x
−
=
20. ( )
3
2 x
q x
+
=

Section 1.5 Transformation of Functions 83
Sketch a graph of each function as a transformation of a toolkit function.
21. f ( t)
2
= ( t +1) − 3
22. h( x) = x −1 + 4
23. k ( x) = ( x − )3
2 −1
24. m( t) = 3+ t + 2
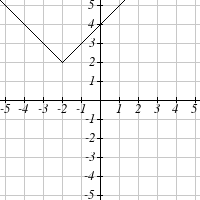
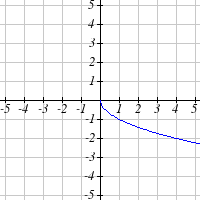
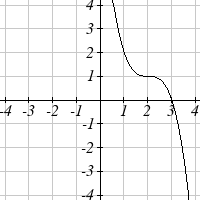
Write an equation for each function graphed below.
25.
26.
27.
28.
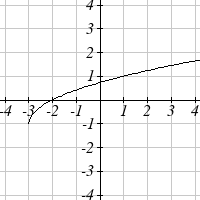
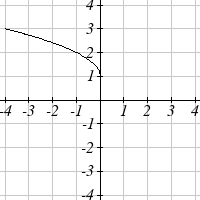
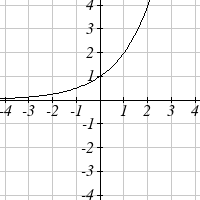
Find a formula for each of the transformations of the square root whose graphs are given
below.
29.
30.

84 Chapter 1
The graph of ( ) 2 x
f x = is shown. Sketch a graph of each
transformation of f ( x)
31. ( )
2 x
g x = − +1
32. ( ) 2 x
h x
−
=
33. Starting with the graph of ( ) 6 x
f x = write the equation of the graph that results from
a. reflecting f ( x) about the x-axis and the y-axis
b. reflecting f ( x) about the x-axis, shifting left 2 units, and down 3 units
34. Starting with the graph of ( ) 4 x
f x = write the equation of the graph that results from
a. reflecting f ( x) about the x-axis
b. reflecting f ( x) about the y-axis, shifting right 4 units, and up 2 units
Write an equation for each function graphed below.
35.
36.
37.
38.
Section 1.5 Transformation of Functions 85
39. For each equation below, determine if the function is Odd, Even, or Neither.
a. f ( x)
4
= 3 x
b. g( x) = x
c. h( x) 1
= + 3 x
x
40. For each equation below, determine if the function is Odd, Even, or Neither.
a. f ( x) = ( x − )2
2
b. g ( x)
4
= 2 x
c. h( x)
3
= 2 x − x
Describe how each function is a transformation of the original function f( x).
41. − f ( x)
42. f (− x)
43. 4 f ( x)
44. 6 f ( x)
45. f (5 x)
46. f (2 x)
47. 1
f
x
48.
1
f x
3
5
49. 3 f (− x)
50. − f (3 x)
Write a formula for the function that results when the given toolkit function is
transformed as described.
51. f ( x) = x reflected over the y axis and horizontally compressed by a factor of 1 .
4
52. f ( x) = x reflected over the x axis and horizontally stretched by a factor of 2.
53.
1
f ( x) =
vertically compressed by a factor of 1 , then shifted to the left 2 units and
2
x
3
down 3 units.
54.
1
f ( x) = vertically stretched by a factor of 8, then shifted to the right 4 units and up
x
2 units.
55.
2
f ( x) = x horizontally compressed by a factor of 1 , then shifted to the right 5 units 2
and up 1 unit.
56.
2
f ( x) = x horizontally stretched by a factor of 3, then shifted to the left 4 units and down 3 units.
86 Chapter 1
Describe how each formula is a transformation of a toolkit function. Then sketch a graph
of the transformation.
57. f ( x) = ( x + )2
4
1 − 5
58. g x = ( x + )2
( ) 5
3 − 2
59. h( x) = 2
− x − 4 + 3
60. k ( x) = 3
− x −1
61. m( x) 1 3
= x
62. n( x) 1
= x − 2
2
3
2
3
63. p( x) 1 x
=
−
1
3
64. q( x) =
x +
1
3
4
65. a( x) = − x + 4
66. b( x) 3
= − x − 6
Determine the interval(s) on which the function is increasing and decreasing.
67. f ( x) = ( x + )2
4
1 − 5
68. g x = ( x + )2
( ) 5
3 − 2
69. a( x) = − x + 4
70. k ( x) = 3
− x −1
Determine the interval(s) on which the function is concave up and concave down.
71. m( x) = − (
2 x + )
3 3 +1
72. b( x) 3
= − x − 6
2
73. p( x) 1 x
=
−
3
74. k ( x) = 3
− x −1
3


Section 1.5 Transformation of Functions 87
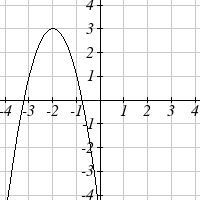
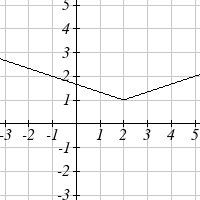
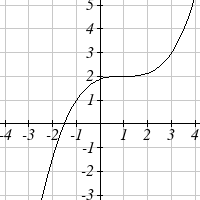
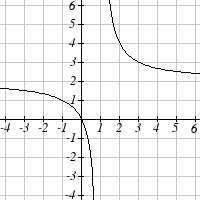
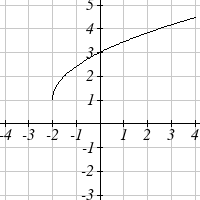
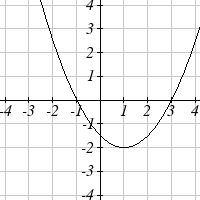
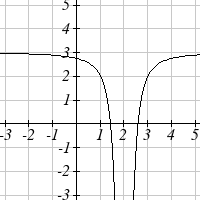
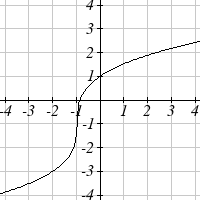
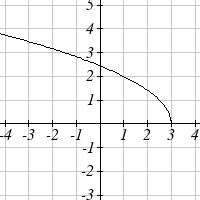
The function f ( x) is graphed here. Write an equation for each
graph below as a transformation of f ( x) .
75.
76.
77.
78.
79.
80.
81.
82.
83.
84.
85.
86.


88 Chapter 1
Write an equation for each transformed toolkit function graphed below.
87.
88.
89.
90.
91.
92.
93.
94.
95.
96.
97.
98.
Section 1.5 Transformation of Functions 89
99. Suppose you have a function y = f ( x) such that the domain of f ( x) is 1 ≤ x ≤ 6 and the range of f ( x) is −3 ≤ y ≤ 5. [UW]
a. What is the domain of f(2( x − 3)) ?
b. What is the range of f ( (
2 x − ))
3 ?
c. What is the domain of 2 f ( x) − 3 ?
d. What is the range of 2 f ( x) − 3 ?
e. Can you find constants B and C so that the domain of f ( B( x − C)) is 8 ≤ x ≤ 9?
f. Can you find constants A and D so that the range of Af ( x) + D is 0 ≤ y ≤ 1?

90 Chapter 1
Section 1.6 Inverse Functions
A fashion designer is travelling to Milan for a fashion show. He asks his assistant, Betty,
what 75 degrees Fahrenheit is in Celsius, and after a quick search on Google, she finds
the formula
5
C = ( F − )
32 . Using this formula, she calculates 5 (75 − 32) ≈ 24degrees
9
9
Celsius. The next day, the designer sends his assistant the week’s weather forecast for
Milan, and asks her to convert the temperatures to Fahrenheit.
At first, Betty might consider using the formula she has already found to do the
conversions. After all, she knows her algebra, and can easily solve the equation for F
after substituting a value for C. For example, to convert 26 degrees Celsius, she could
write: 5
26 = ( F ?











































