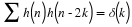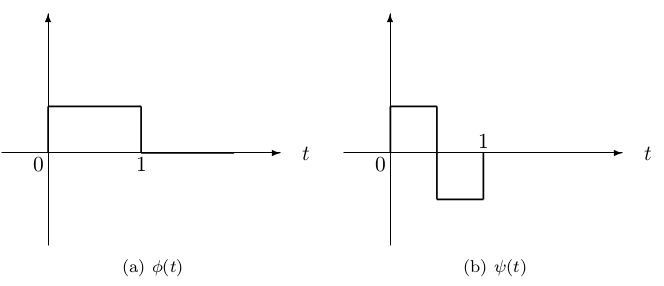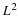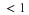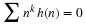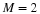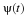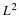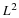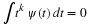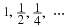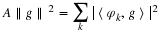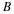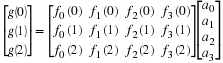2013/02/11 14:59:02 -0600
In this chapter, we develop the properties of wavelet systems in terms of the underlying filter banks associated with them. This is an expansion and elaboration of the material in Chapter: Filter Banks and the Discrete Wavelet Transform , where many of the conditions and properties developed from a signal expansion point of view in Chapter: The Scaling Function and Scaling Coefficients, Wavelet and Wavelet Coefficients are now derived from the associated filter bank. The Mallat algorithm uses a special structure of filters and downsamplers/upsamplers to calculate and invert the discrete wavelet transform. Such filter structures have been studied for over three decades in digital signal processing in the context of the filter bank and transmultiplexer problems 28, 31, 37, 33, 34, 36, 21, 32, 25. Filter bank theory, besides providing efficient computational schemes for wavelet analysis, also gives valuable insights into the construction of wavelet bases. Indeed, some of the finer aspects of wavelet theory emanates from filter bank theory.
A filter bank is a structure that decomposes a signal into a collection of subsignals. Depending on the application, these subsignals help emphasize specific aspects of the original signal or may be easier to work with than the original signal. We have linear or non-linear filter banks depending on whether or not the subsignals depend linearly on the original signal. Filter banks were originally studied in the context of signal compression where the subsignals were used to “represent” the original signal. The subsignals (called subband signals) are downsampled so that the data rates are the same in the subbands as in the original signal—though this is not essential. Key points to remember are that the subsignals convey salient features of the original signal and are sufficient to reconstruct the original signal.
Figure 9.1 shows a linear filter bank that is used in signal compression (subband coding). The analysis filters {hi} are used to filter the input signal x(n). The filtered signals are downsampled to give the subband signals. Reconstruction of the original signal is achieved by upsampling, filtering and adding up the subband signals as shown in the right-hand part of Figure 9.1. The desire for perfect reconstruction (i.e., y(n)=x(n)) imposes a set of bilinear constraints (since all operations in Figure 9.1 are linear) on the analysis and synthesis filters. This also constrains the downsampling factor, M, to be at most the number of subband signals, say L. Filter bank design involves choosing filters {hi} and {gi} that satisfy perfect reconstruction and simultaneously give informative and useful subband signals. In subband speech coding, for example, a natural choice of desired frequency responses—motivated by the nonuniform sensitivity of the human ear to various frequency bands—for the analysis and synthesis filters is shown in Figure 9.2.
In summary, the filter bank problem involves the design of the filters hi(n) and gi(n), with the following goals:
Perfect Reconstruction (i.e., y(n)=x(n)).
Usefulness. Clearly this depends on the application. For the subband coding application, the filter frequency responses might approximate the ideal responses in Figure 9.2. In other applications the filters may have to satisfy other constraints or approximate other frequency responses.
If the signals and filters are multidimensional in Figure 9.1, we have the multidimensional filter bank design problem.
A transmultiplexer is a structure that combines a collection of signals into a single signal at a higher rate; i.e., it is the dual of a filter bank. If the combined signal depends linearly on the constituent signal, we have a linear transmultiplexer. Transmultiplexers were originally studied in the context of converting time-domain-multiplexed (TDM) signals into frequency domain multiplexed (FDM) signals with the goal of converting back to time-domain-multiplexed signals at some later point. A key point to remember is that the constituent signals should be recoverable from the combined signal. Figure 9.3 shows the structure of a transmultiplexer. The input signals yi(n) were upsampled, filtered, and combined (by a synthesis bank of filters) to give a composite signal d(n). The signal d(n) can be filtered (by an analysis bank of filters) and downsampled to give a set of signals xi(n). The goal in transmultiplexer design is a choice of filters that ensures perfect reconstruction (i.e., for all i, xi(n)=yi(n)). This imposes bilinear constraints on the synthesis and analysis filters. Also, the upsampling factor must be at least the number of constituent input signals, say L. Moreover, in classical TDM-FDM conversion the analysis and synthesis filters must approximate the ideal frequency responses in Figure 9.2. If the input signals, analysis filters and synthesis filters are multidimensional, we have a multidimensional transmultiplexer.
We now take a closer look at the set of bilinear constraints on the analysis and synthesis filters of a filter bank and/or transmultiplexer that ensures perfect reconstruction (PR). Assume that there are L analysis filters and L synthesis filters and that downsampling/upsampling is by some integer M. These constraints, broadly speaking, can be viewed in three useful ways, each applicable in specific situations.
Direct characterization - which is useful in wavelet theory (to characterize orthonormality and frame properties), in the study of a powerful class of filter banks (modulated filter banks), etc.
Matrix characterization - which is useful in the study of time-varying filter banks.
z-transform-domain (or polyphase-representation) characterization - which is useful in the design and implementation of (unitary) filter banks and wavelets.
We will first consider the direct characterization of PR, which, for both filter banks and transmultiplexers, follows from an elementary superposition argument.
Theorem 38 A filter bank is PR if and only if, for all integers n1 and n2,
A transmultiplexer is PR if and only if, for all i,j∈{0 , 1 , ... , L – 1},
Moreover, if the number of channels is equal to the downsampling factor (i.e., L=|M|),Equation 9.1 and Equation 9.2 are equivalent.
Consider a PR filter bank. Since an arbitrary signal is a linear superposition of impulses,
it suffices to consider the input signal,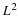 
, for arbitrary integer n1. Then
(see Figure 9.1) 
and therefore,
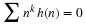. But by PR,
.
The filter bank PR property is precisely a statement of this fact:
Consider a PR transmultiplexer. Once again because of linear superposition, it suffices
to cosnsider only the input signals xi(n)=δ(n)δ(i–j) for all i and j. Then,
d(n)=gj(n) (see Figure 9.3), and 
. But by PR yi(l)=δ(l)δ(i–j).
The transmultiplexer PR property is precisely a statement of this fact:
Remark: Strictly speaking, in the superposition argument proving Equation 9.2, one has to consider the input signals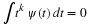 
for arbitrary n1. One readily verifies that for all n1
Equation 9.2 has to be satisfied.
The equivalence of Equation 9.1 and Equation 9.2 when L=M is not obvious from the direct characterization. However, the transform domain characterization that we shall see shortly will make this connection obvious. For a PR filter, bank the L channels should contain sufficient information to reconstruct the original signal (note the summation over i in Equation 9.1), while for a transmultiplexer, the constituent channels should satisfy biorthogonality constraints so that they can be reconstructed from the composite signal (note the biorthogonality conditions suggested by Equation 9.2).
The second viewpoint is linear-algebraic in that it considers all signals as vectors and all filtering operations as matrix-vector multiplications 34. In Figure 9.1 and Figure 9.3 the signals x(n), di(n) and y(n) can be naturally associated with infinite vectors x, di and y respectively. For example, x=[⋯,x(–1),x(0),x(1),⋯]. Then the analysis filtering operation can be expressed as
where, for each i, Hi is a matrix with entries appropriately drawn from filter hi. Hi is a block Toeplitz matrix (since its obtained by retaining every Mth row of the Toeplitz matrix representing convolution by hi) with every row containing hi in an index-reversed order. Then the synthesis filtering operation can be expressed as
where, for each i, Gi is a matrix with entries appropriately drawn from filter gi.
Gi is also a block Toeplitz matrix (since it is obtained by retaining every Mth row
of the Toeplitz matrix whose transpose represents convolution by gi) with every row containing gi in its natural order.
Define d to be the vector obtained by interlacing the entries of each of the vectors di:
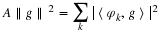. Also define the
matrices H and G (in terms of Hi and Gi) so that
H is obtained by interlacing the rows of Hi and G is obtained by interlacing the rows of Gi. For example, in the FIR case if the filters are all of length N,
From this development, we have the following result:
Theorem 39 A filter bank is PR iff
A transmultiplexer is PR iff
Moreover, when L=M, both conditions are equivalent.
One can also write the PR conditions for filter banks and transmultiplexers in the following form, which explicitly shows the formal relationship between the direct and matrix characterizations. For a PR filter bank we have