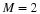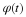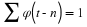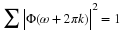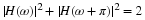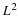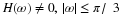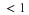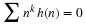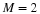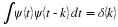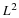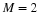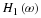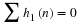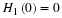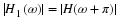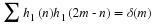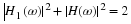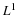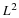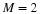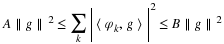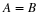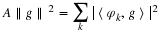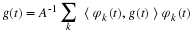A set of vectors or functions f_k(t)spans a vector space F (or F is the Span of the set) if any element of that space can be expressed as a linear combination of members of that set, meaning: Given the finite or infinite set of functions f_k(t), we define 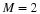as the vector space with all elements of the space of the form

(5.1)

with k∈Z and t,a∈R. An inner product is usually defined for this space and is denoted 〈f(t),g(t)〉. A norm is defined and is denoted by .

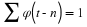We say that the set f_k(t) is a basis set or a basis for a given space F if the set of in Equation 5.1 are unique for any particular g(t)∈F. The set is called an orthogonal basis if 〈f_k(t),f_ℓ(t)〉=0 for all k≠ℓ. If we are in three dimensional Euclidean space, orthogonal basis vectors are coordinate vectors that are at right (90^o) angles to each other. We say the set is an orthonormal basis if 〈f_k(t),f_ℓ(t)〉=δ(k–ℓ) i.e. if, in addition to being orthogonal, the basis vectors are normalized to unity norm: ∥f_k(t)∥=1 for all k.

From these definitions it is clear that if we have an orthonormal basis, we can express any element in the vector space, g(t)∈F, written as Equation 5.1 by

(5.2)

since by taking the inner product of f_k(t) with both sides of Equation 5.1, we get

(5.3)

where this inner product of the signal g(t) with the basis vector f_k(t) “picks out" the corresponding coefficient a_k. This expansion formulation or representation is extremely valuable. It expresses Equation 5.2 as an identity operator in the sense that the inner product operates on g(t) to produce a set of coefficients that, when used to linearly combine the basis vectors, gives back the original signal g(t). It is the foundation of Parseval's theorem which says the norm or energy can be partitioned in terms of the expansion coefficients a_k. It is why the interpretation, storage, transmission, approximation, compression, and manipulation of the coefficients can be very useful. Indeed, Equation 5.2 is the form of all Fourier type methods.

Although the advantages of an orthonormal basis are clear, there are cases where the basis system dictated by the problem is not and cannot (or should not) be made orthogonal. For these cases, one can still have the expression of Equation 5.1 and one similar to Equation 5.2 by using a dual basis set whose elements are not orthogonal to each other, but to the corresponding element of the expansion set

(5.4)

Because this type of “orthogonality" requires two sets of vectors, the expansion set and the dual set, the system is called biorthogonal. Using Equation 5.4 with the expansion in Equation 5.1 gives

(5.5)

Although a biorthogonal system is more complicated in that it requires, not only the original expansion set, but the finding, calculating, and storage of a dual set of vectors, it is very general and allows a larger class of expansions. There may, however, be greater numerical problems with a biorthogonal system if some of the basis vectors are strongly correlated.

The calculation of the expansion coefficients using an inner product in Equation 5.3 is called the analysis part of the complete process, and the calculation of the signal from the coefficients and expansion vectors in Equation 5.1 is called the synthesis part.

In finite dimensions, analysis and synthesis operations are simply matrix–vector multiplications. If the expansion vectors in Equation 5.1 are a basis, the synthesis matrix has these basis vectors as columns and the matrix is square and non singular. If the matrix is orthogonal, its rows and columns are orthogonal, its inverse is its transpose, and the identity operator is simply the matrix multiplied by its transpose. If it is not orthogonal, then the identity is the matrix multiplied by its inverse and the dual basis consists of the rows of the inverse. If the matrix is singular, then its columns are not independent and, therefore, do not form a basis.

Matrix Examples

Using a four dimensional space with matrices to illustrate the ideas of this chapter, the synthesis formula becomes

(5.6)

which can be compactly written in matrix form as

(5.7)

The synthesis or expansion Equation 5.1 or Equation 5.7 becomes

(5.8)

with the left-hand column vector g being the signal vector, the matrix F formed with the basis vectors f_k as columns, and the right-hand vector a containing the four expansion coefficients, a_k.

The equation for calculating the k^th expansion coefficient in Equation 5.6 is

(5.9)

which can be written in vector form as

(5.10)

where each a_k is an inner product of the k^th row of 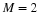with g and analysis or coefficient Equation 5.3 or Equation 5.10 becomes

(5.11)

which together are Equation 5.2 or

(5.12)

Therefore,

(5.13)

is how the dual basis in Equation 5.4 is found.

If the columns of F are orthogonal and normalized, then

(5.14)

This means the basis and dual basis are the same, and Equation 5.12 and Equation 5.13 become

(5.15)

and

(5.16)

which are both simpler and more numerically stable than Equation 5.13.

The discrete Fourier transform (DFT) is an interesting example of a finite dimensional Fourier transform with orthogonal basis vectors where matrix and vector techniques can be informative as to the DFT's characteristics and properties. That can be found developed in several signal processing books.

Fourier Series Example

The Fourier Series is an excellent example of an infinite dimensional composition (synthesis) and decomposition (analysis). The expansion formula for an even function g(t) over 0<x<2π is

(5.17)

where the basis vectors (functions) are

(5.18) f_k ( t ) = cos ( k t )

and the expansion coefficients are obtained as

(5.19)

The basis vector set is easily seen to be orthonormal by verifying

(5.20)

These basis functions span an infinite dimensional vector space and the convergence of Equation 5.17 must be examined. Indeed, it is the robustness of that convergence that is discussed in this section under the topic of unconditional bases.

Sinc Expansion Example

Another example of an infinite dimensional orthogonal basis is Shannon's sampling expansion 9. If f(t) is band limited, then

(5.21)

for a sampling interval 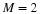if the spectrum of f(t) is zero for |ω|>W. In this case the basis functions are the sinc functions with coefficients which are simply samples of the original function. This means the inner product of a sinc basis function with a bandlimited function will give a sample of that function. It is easy to see that the sinc basis functions are orthogonal by taking the inner product of two sinc functions which will sample one of them at the points of value one or zero.

While the conditions for a set of functions being an orthonormal basis are sufficient for the representation in Equation 5.2 and the requirement of the set being a basis is sufficient for Equation 5.5, they are not necessary. To be a basis requires uniqueness of the coefficients. In other words it requires that the set be independent, meaning no element can be written as a linear combination of the others.

If the set of functions or vectors is dependent and yet does allow the expansion described in Equation 5.5, then the set is called a frame. Thus, a frame is a spanning set. The term frame comes from a definition that requires finite limits on an inequality bound 2, 12 of inner products.

If we want the coefficients in an expansion of a signal to represent the signal well, these coefficients should have certain properties. They are stated best in terms of energy and energy bounds. For an orthogonal basis, this takes the form of Parseval's theorem. To be a frame in a signal space, an expansion set ϕ_k(t) must satisfy

(5.22)

for some 0<A and B<∞ and for all signals g(t) in the space. Dividing Equation 5.22 by ∥g∥² shows that A and B are bounds on the normalized energy of the inner products. They “frame" the normalized coefficient energy. If

(5.23)

then the expansion set is called a tight frame. This case gives

(5.24)

which is a generalized Parseval's theorem for tight frames. If A=B=1, the tight frame becomes an orthogonal basis. From this, it can be shown that for a tight frame 2

(5.25)

which is the same as the expansion using an orthonormal basis except for the A^–1 term which is a measure of the redundancy in the expansion set.

If an expansion set is a non tight frame, there is no strict Parseval's theorem and the energy in the transform domain cannot be exactly partitioned. However, the closer A and B are, the better an approximate partitioning can be done. If A=B, we have a tight frame and the partitioning can be done exactly with Equation 5.24. Daubechies 2 shows that the tighter the frame bounds in Equation 5.22 are, the better the analysis and synthesis system is conditioned. In other words, if