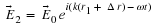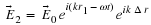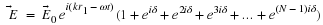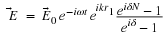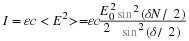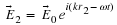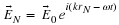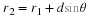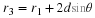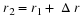Figure 8.1. 

Refraction at a spherical interface. Click on image for larger version.

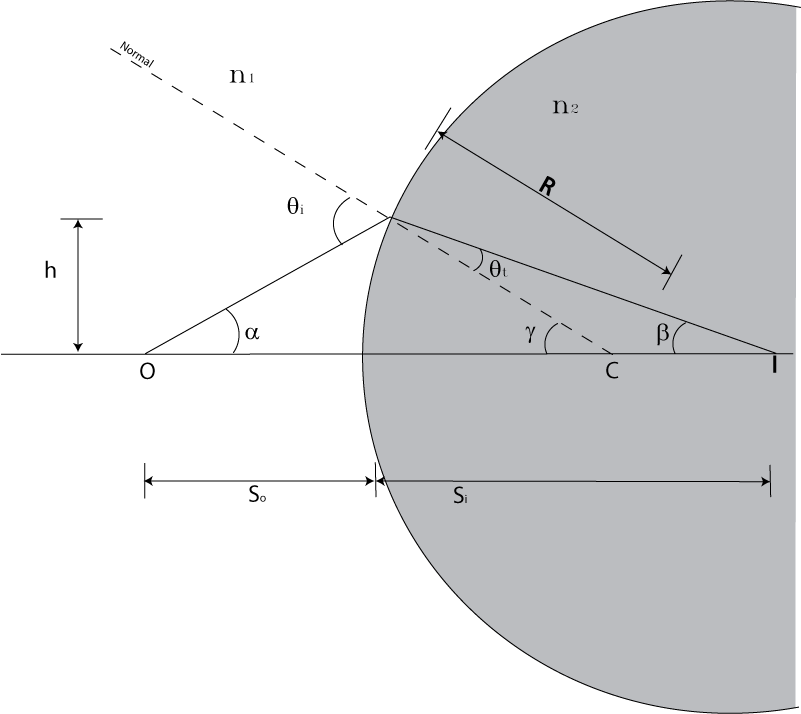
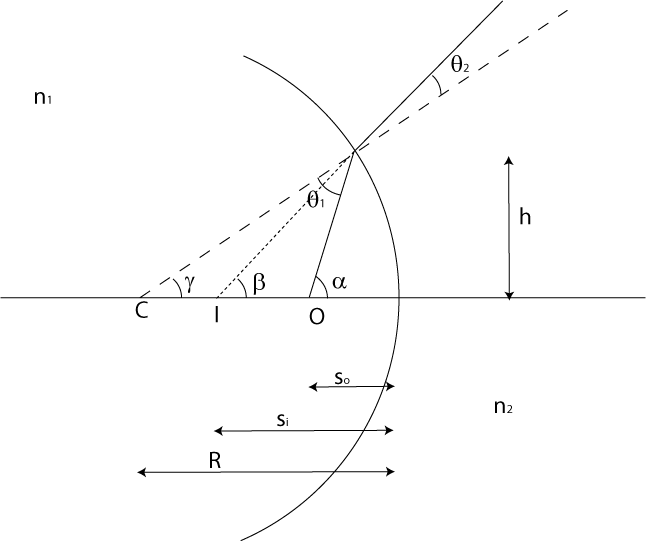
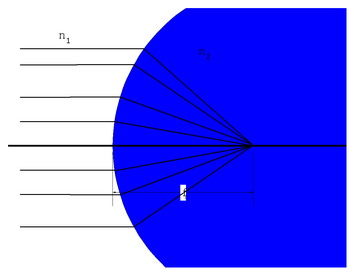
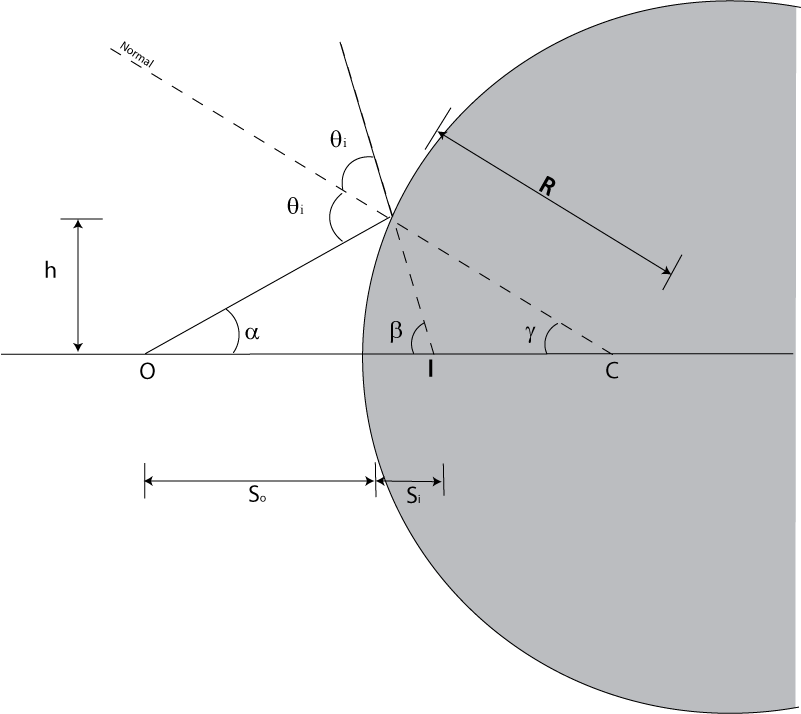
Look at the figure showing refraction at a sphere.In this figure:

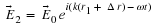
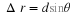
There is a ray that strikes the surface at height h. In general rays hitting the surface at different points will be bent to different points along the optical axis. However for small angles we will show they all converge at the same point.So lets use the small angle approximation 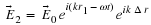Now from trigonometry we can see that: θ_i = α + γ γ = θ_t + β or θ_t = γ − β now Snell's law says n₁ sin θ_i = n₂ sin θ_t or n₁θ_i ≈ n₂θ_t n₁ ( α + γ ) = n₂ ( γ − β ) γ ( n₂ − n₁ ) = n₂β + n₁α Now all the h 's cancel so there is no dependence on point on surface. That is: Now lets consider the case of a concave surface. The picture is

Figure 8.2. 

Click to get larger image.

Again we use the small angle approximation and thus we have n₁θ₁ = n₂θ₂ In this case we also see that α = θ₁ + γ and β = θ₂ + γ so we can write n₁ ( α − γ ) = n₂ ( β − γ ) or or

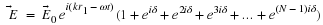
However we can make the equation identical to the previous one if we adopt the following sign convention:

Then the equation becomes as before

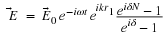
In this case note that the image is imaginary (whereas in the first case it was real). Note that the actual rays pass through a real image.

The focal point is the object point which causes the image to occur at infinity.

Figure 8.3. 

That is all the rays end up traveling parallel to each other. In this case s_i goes to ∞ so becomes or

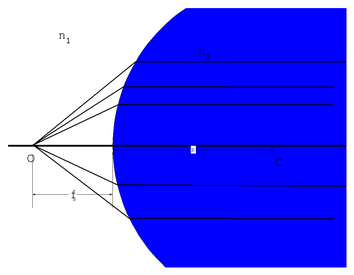
Now we can find a focal point to the right of the of the surface by considering parallel rays coming in from the left.

Figure 8.4. 

Then we get 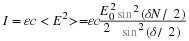But we do have to expand our sign conventionfor light incident from the left

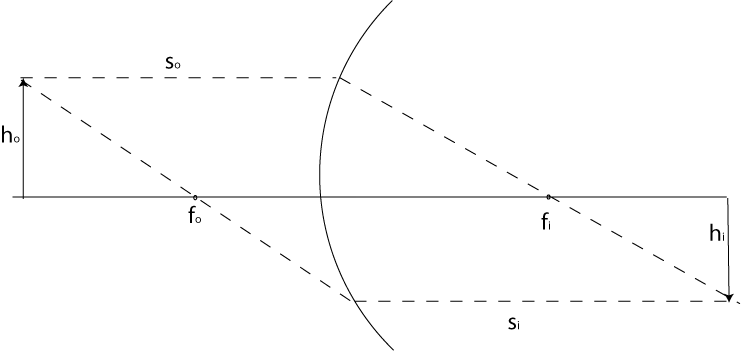
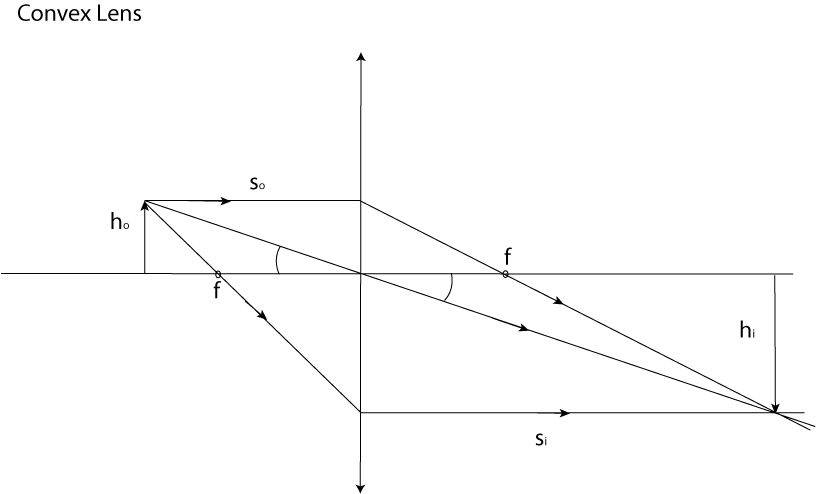
With the definition of focal points, we also have a natural way to graphically solve optical problems. Any ray drawn horizontally from the left side of the interface will pass through the focal point on the right. Any ray going through the focal point on the left will go horizontally on the right. The following figure illustrates this.

Figure 8.5. 

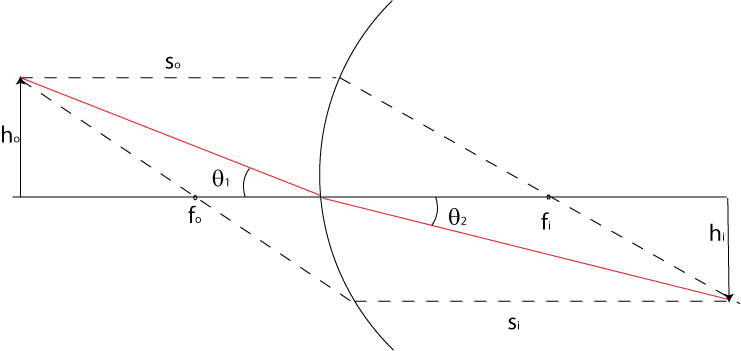
The magnification of the image is the ratio of the heights h_o to h_i.

Figure 8.6. 

Since we are using the small angle approximation, we have Snell's law n₁θ₁ = n₂θ₂ which can be rewritten 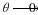So we write that the magnification is 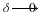The negative sign is introduced to capture the fact that the image is inverted. It is worth pointing out that in our diagram above, the image is real, because the actual light rays pass through it.

Now we can turn to the case of lenses. A lens can be considered the combination of two spherical interfaces. To solve an optical problem using multiple interfaces or lenses, one considers each one by one. For example one finds the image created by the first surface and then uses it as the object of the second surface.

Figure 8.7. 

Consider a lens of thickness d as shown in the drawing. At interface 1 (coloured red in the drawing) we have 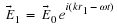For surface 2 (coloured blue) the image of the the first surface becomes the object of the second. Note the sign of s_o2 is negative so that s_o2 = d − s_i1Thus 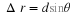becomes 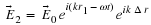Now add the equations

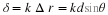
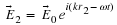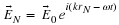
Now we take the thin lens case,that is d → 0 That equation would work for making prescription swim goggles for example, however most of the time n₁ = n₃ (namely air for eyeglasses). So making that the case we get which in the case of air (n=1) is That is The lensmaker's formula(where n_l is the index of refraction of the lens material)Now we can find the foci 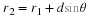Which we see from the lensmaker's formula must be the same so lets drop the subscripts: 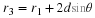and 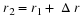which is the Gaussian Lens Formula

A convex lens will have a positive focal length f .

Figure 8.8. 

We can use the same equation as before for the magnification, 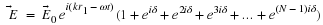but now note that n₁ = n₂ so the equation becomes

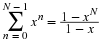You can examine the figure above to verify that this is true.

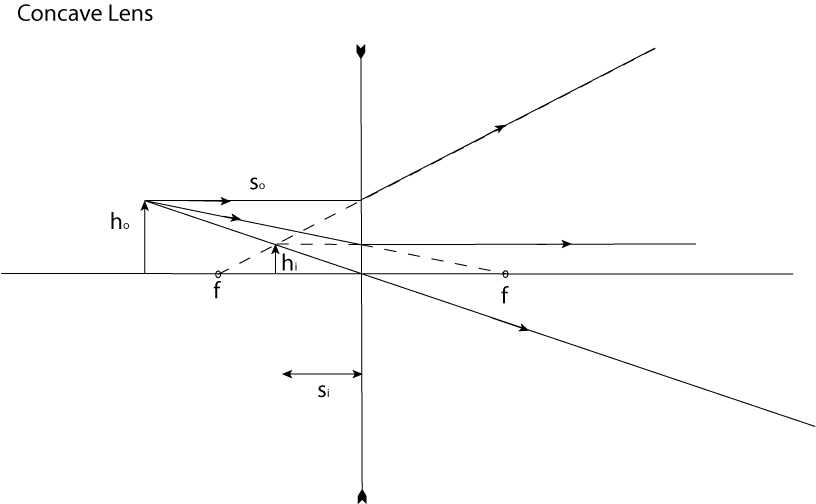
We can also consider a concave lens which has a negative focal length. Notice that in this case the image is upright and virtual. Notice that in this case s_i is negative.

Figure 8.9. 

Figure 8.10. 

Notice that in Mirrors we get a virtual image to the right of the surface. Thus for mirrors we say that s_i is positive to the left of the mirror. This allows to retain correspondence between s_i being negative and an image being virtual.

Again we use the small angle approximation. By inspection of the figure we see that 2 θ_i = α + β and θ_i = α + γ . Now we multiply the second equation by two and subtract the first equation from it and we get: 2 α + 2 γ − α − β = 0 or α − β = − 2 γ . Using the small angle approximation we see that this is 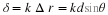where I have used the fact that s_i is negative to the right of the mirror. So I can write the mirror equation as 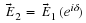or where for a mirror 1 / f = − 2 / R

First a little nomenclature. Optometrists (and opthamologists) use the dioptric power measured in diopters. A diopter is 1 / f where f is measured in meters. The focal length of lenses in contact is or using dioptric power D = D₁ + D₂ A "normal" eye will focus an object at infinity onto the r