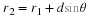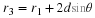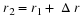Divergence, Gradient and Curl
Assume we have measured the temperature in a room along an axis
x
.
If we wanted to find the temperature change as we move to postion
(
x
+
Δ
x
)
then from the fundamental definition of a derivative we know that is:
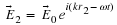
We can easily extend this concept to 3 dimensions At position
(
x
,
y
,
z
)
there is a temperature
T
(
x
,
y
,
z
)
.
Suppose we then want to find the temperature at
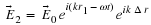 .
Then we can
use:
.
Then we can
use: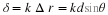
We could define a vector
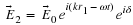 and then say
and then say
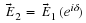 so let's define an operator
so let's define an operator
 Then we can write
Then we can write
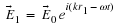
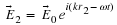 is a vector operator that can be used in other situations involving scalars
and vectors. It is often named "del" or "nabla". Operating on a scalar field
with this operator is called taking the "gradient" of the field.
is a vector operator that can be used in other situations involving scalars
and vectors. It is often named "del" or "nabla". Operating on a scalar field
with this operator is called taking the "gradient" of the field.
We could also operate on a vector field with del. There are two different ways
to do this, by taking the dot and the cross products. To operate on a vector
field by taking its dot product with del is referred to as taking the
divergence. ie.
 where
where
 is some vector field and
f
is the resulting scalar field.
is some vector field and
f
is the resulting scalar field.
Similarly one could take the cross product:
 where
where
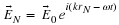 is the resulting vector field.
is the resulting vector field.
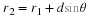 This
is referred to as taking the curl of a field.
This
is referred to as taking the curl of a field.
These operations, Gradient, Divergence and Curl are of fundamental importance.
They have been presented above as operations using some newly defined operator
but they in fact have deep physical significance. When using these operators
to express Maxwell's equations in differential form, the meaning of these
operations will hopefully become more clear. Gradient is the easiest to
understand, it can be thought of as a three dimensional slope.
Having defined these operations we can go on to second derivative type things
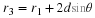 Note
that
∇2
occurs so often that is has its own name, Laplacian
Note
that
∇2
occurs so often that is has its own name, Laplacian

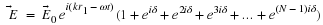

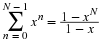
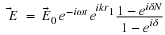 Here is an example of taking a divergence that will be extremely useful.
If
Here is an example of taking a divergence that will be extremely useful.
If
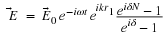 and
and
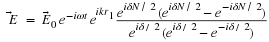 and
and
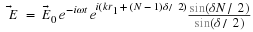 then
lets find (for
then
lets find (for
 is a constant vector)
is a constant vector)