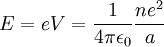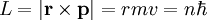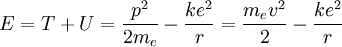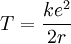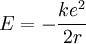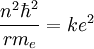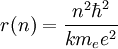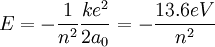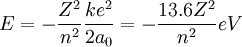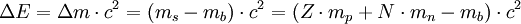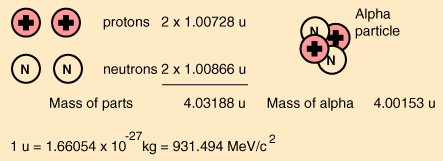999.6
2,260
3,375
4,565
6,950
8,490
27,107
Cl
1,256
2,295
3,850
5,160
6,560
9,360
11,000
Ar
1,520
2,665
3,945
5,770
7,230
8,780
12,000
Application
In order to determine how many electrons are in the outermost shell of an element, one
can use the ionization energy. If, for example, it required 1,500 kJ/mol to remove one
mole of electrons and required 6,000 kJ/mol to remove another mole of electrons and
then 5,000 kJ/mol, etc. this means that the element had one electron in its outermost
shell. This means that the element is a metal and in order for this element to achieve
a stable complete outer shell, it needs to lose one electron. Thus, the first electron is
easy to remove and consequently the ionization energy is low. Notice, however, that
once the stable complete outer shell has been formed, it becomes much more difficult
to remove the next electron. If that electron can be removed the consequent one can
be removed a bit more easily.


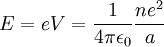
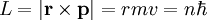
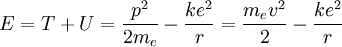
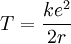
African Virtual University
Electrostatic explanation
Atomic ionization energy can be predicted by an analysis using electrostatic potential
and the Bohr model of the atom, as follows.
Consider an electron of charge -e, and an ion with charge +ne, where n is the number of electrons missing from the ion. According to the Bohr model, if the electron were
to approach and bind with the atom, it would come to rest at a certain radius a. The
electrostatic potential V at distance a from the ionic nucleus, referenced to a point infinitely far away, is:
Since the electron is negatively charged, it is drawn to this positive potential. (The
value of this potential is called the ionization potential). The energy required for it
to «climb out» and leave the atom is:
This analysis is incomplete, as it leaves the distance a as an unknown variable. It can
be made more rigorous by assigning to each electron of every chemical element a
characteristic distance, chosen so that this relation agrees with experimental data.
It is possible to expand this model considerably by taking a semi-classical approach,
in which momentum is quantized. This approach works very well for the hydrogen
atom, which only has one electron. The magnitude of the angular momentum for a
circular orbit is:
The total energy of the atom is the sum of the kinetic and potential energies, that is:
Velocity can be eliminated from the kinetic energy term by setting the Coulomb
attraction equal to the centripetal force, giving:

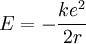
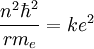
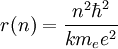
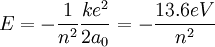
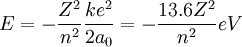
African Virtual University
Now the energy can be found in terms of k, e, and r. Using the new value for the kinetic energy in the total energy equation above, it is found that:
Solving the angular momentum for v and substituting this into the expression for
kinetic energy, we have:
This establishes the dependence of the radius on n. That is:
At its smallest value, n is equal to 1 and r is the Bohr radius a . Now, the equation 0
for the energy can be established in terms of the Bohr radius. Doing so gives the
result:
This can be expanded to larger nuclei by incorporating the atomic number into the
equation.

African Virtual University
Electron Affinity (EA).
The electron affinity, ( E A), of an atom or molecule is the energy required to detach an electron from a singly charged negative ion, i.e., the energy change for the process
X- → X + e−
An equivalent definition is the energy released ( E
− E ) when an electron is
initial
final
attached to a neutral atom or molecule. It should be noted that the sign convention
for E is the opposite to most thermodynamic quantities: a positive electron affinity
ea
indicates that energy is released on going from atom to anion.
All elements whose EA have been measured using modern methods have a positive
electron affinity, but older texts mistakenly report that some elements such as alkaline
earth metals have negative E , meaning they would repel electrons. The electron
ea
affinity of the noble gases have not been conclusively measured, so they may or
may not have slightly negative EAs. Atoms whose anions are relatively more stable
than neutral atoms have a greater E . Chlorine most strongly attracts extra electrons;
ea
mercury most weakly attracts an extra electron. E of noble gases are close to 0.
ea
Although E vary in a chaotic manner across the table, some patterns emerge. Ge-
ea
nerally, nonmetals have more positive E than metals.
ea
E is not limited to the elements but also applies to molecules. For instance the elec-
ea
tron affinity for benzene is negative, as is that of naphthalene.
n.B. Don’t confuse Electron affinity with work function. The work function is the
minimum energy (usually measured in electron volts) needed to remove an electron
from a solid to a point immediately outside the solid surface (or energy needed to
move an electron from the Fermi energy level into vacuum). Here «immediately»
means that the final electron position is far from the surface on the atomic scale but
still close to the solid on the macroscopic scale. The work function is an important
property of metals. The magnitude of the work function is usually about a half of the
ionization energy of a free atom of the metal.
Nuclear binding energies
Nuclear binding energy is derived from the strong nuclear force and is the energy
required to disassemble a nucleus into free unbound neutrons and protons, strictly so
that the relative distances of the particles from each other are infinite (essentially far
enough so that the strong nuclear force can no longer cause the particles to interact).
At the atomic level, the binding energy of the atom is derived from electromagnetic
interaction and is the energy required to disassemble an atom into free electrons and
a nucleus.

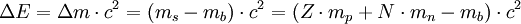
African Virtual University
The binding energy for a single nucleus is given by
where
c is the speed of light;
m is the mass of the separated nucleons;
s
m is the mass of the bound nucleus;
b
Z is the atomic number of the bound nucleus;
m is the mass of one proton;
p
N is the number of neutrons;
m is the mass of one neutron.
n
In atoms with high or very low ratios of protons to neutrons, the binding energy
becomes negative, resulting in an unstable nucleus.
Specific example: a deuteron
A deuteron is the nucleus of a deuterium atom, and consists of one proton and one
neutron. The experimentally-measured masses of the constituents as free particles
are
m
= 1.007825 u;
proton
m
= 1.008665 u;
neutron
m
+ m
= 1.007825 + 1.008665 = 2.01649 u.
proton
neutron
The mass of the deuteron (also an experimentally measured quantity) is
Atomic mass 2H = 2.014102 u.
The mass difference = 2.01649−2.014102 u = 0.002388 u. Since the conversion
between rest mass and energy is 931.494MeV/u, a deuteron’s binding energy is
calculated to be
0.002388 u × 931.494 MeV/u = 2.224 MeV.
Thus, expressed in another way, the binding energy is [0.002388/2.01649] x 100%
= about 0.1184% of the total energy corresponding to the mass. This corresponds to
1.07 x 1014 J/kg = 107 TJ/kg.

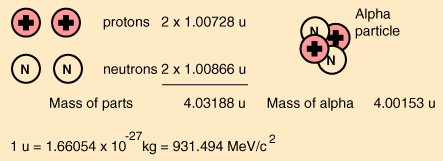

African Virtual University
For the alpha particle Δm= 0.0304 u which gives a binding energy of 28.3 MeV.
The enormity of the nuclear binding energy can perhaps be better appreciated by
comparing it to the binding energy of an electron in an atom. The comparison of the
alpha particle binding energy with the binding energy of the electron in a hydrogen
atom is shown below. The nuclear binding energies are on the order of a million times
greater than the electron binding energies of atoms.

African Virtual University
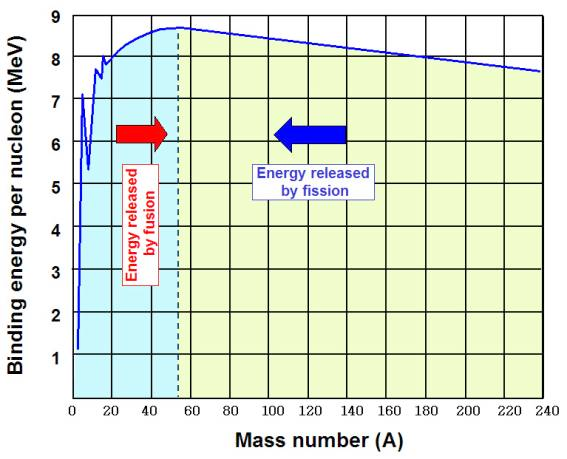
figure 2.6. nuclear binding energy curve
In the periodic table, elements, exhibit a general increase in binding energy per nu-
cleon as the atomic mass increases. This increase is generated by increasing forces
per nucleon in the nucleus, as each additional nucleon is attracted by all of the other
nucleons, and thus more tightly bound to the whole.
The region of increasing binding energy is followed by a region of relative stability
(saturation) in the sequence from magnesium through xenon. In this region, the
nucleus has become large enough that nuclear forces no longer completely extend
efficiently across its width. Attractive nuclear forces in this region, as atomic mass
increases, are nearly balanced by repellent electromagnetic forces between protons,
as atomic number increases.
Finally, in elements heavier than xenon, there is a decrease in binding energy per
nucleon as atomic number increases. In this region of nuclear size, electromagnetic
repulsive forces are beginning to gain against the strong nuclear force.
At the peak of binding energy, nickel-62 is the most tightly-bound nucleus, followed
by iron-58 and iron-56 (This is the basic reason why iron and nickel are very com-
mon metals in planetary cores, since they are produced profusely as end products in
supernovae).

African Virtual University
The existence of a maximum in binding energy in medium-sized nuclei is a conse-
quence of the trade-off in the effects of two opposing forces which have different
range characteristics. The attractive nuclear force (strong nuclear force), which binds
protons and neutrons equally to each other, has a limited range due to a rapid expo-
nential decrease in this force with distance. However, the repelling electromagnetic
force, which acts between protons to force nuclei apart, falls off with distance much
more slowly (as the inverse square of distance). For nuclei larger than about four
nucleons in diameter, the additional repelling force of additional protons more than
offsets any binding energy which results between further added nucleons as a result
of additional strong force interactions; such nuclei become less and less tightly bound
as their size increases, though most of them are still stable. Finally, nuclei containing
more than 209 nucleons (larger than about 6 nucleons in diameter) are all too large
to be stable, and are subject to spontaneous decay to smaller nuclei.
Effective Nuclear charge
Definition: The effective nuclear charge, also known as the kernel charge, is the
net positive charge experienced by an electron in a multi-electron atom. The term
«effective» is used because the shielding effect of negative electrons prevents higher
orbital electrons from experiencing the full nuclear charge.
In an atom with one electron, that electron experiences the full charge of the positive
nucleus. In this case, the electron experiences the charge as it is from the nucleus
without any interference. However, in an atom with many electrons the outer electrons
are simultaneously attracted to the positive nucleus and repelled by the negatively
charged electrons. The effective nuclear charge on such an electron is given by the
following equation:
Z = Z − S
eff
Where ; Z is the number of protons in the nucleus and S is the average number of
electrons between the nucleus and the electron in question,
note: Z is also often known as « Z* ».
eff
A simple way to calculate the effective nuclear charge is to take the total protons
minus all electrons excluding the valence electrons.
Consider a fluorine atom with a +9 nuclear charge and electronic configuration of
1s22s22p5. The two electrons (1s2) in the first energy level as they look at the nucleus
feel a +9 charge because that is the charge on the nucleus. But the electrons that are in
the valence energy level (2s22p5) would be shielded from the nucleus by the 2 shiel-
ding electrons. The +9 nuclear charge is shielded by 2 electrons to give an effective
nuclear charge of +7 that is felt by the valence electrons. If you get out beyond the
valence electrons, then the effective charge is 0 simply because the +9 charge of the
nucleus is surrounded by 9 electrons.

African Virtual University
Trends
down the Periodic Table (Top to Bottom), effective Nuclear Charge for the outer-
most valence electron remains constant moving down a column or family.
Across the Periodic Table (left to Right)
Effective Nuclear Charge increases, going across the Periodic Table. Elements have
more protons and the same number of core electrons.
The increase in the electrostatic force provided by the protons is greater than the
increase in repulsion due to shielding and distance. Therefore, across the Periodic
Table, Effective Nuclear Charge increases.
These trends can be used to explain other trends between elements. Properties such
as atomic radius, Melting and Boiling Points, electronegativity and ionization energy
can be discussed using the Effective Nuclear Charge theory.
Generally, as Z increases:
eff
1) Atomic Radii decrease (Greater pull on electrons means that they are held on
«tighter») but only as you move from the left to the right of the periodic table;
atomic radii increase from top to bottom because of added shells (despite the
decreasing Z )
eff
2) Melting and Boiling Points increase (Higher intermolecular forces as a result of
high Z means that more energy is needed to break intermolecular forces)
eff
3) Electronegativity increases (Directly related to Z )
eff
4) Ionization energy increases (If Z is the net positive force pulling force experien-
eff
ced by an electron, and the ionization energy is the energy required to remove
the outer most electron, the more Z , the more energy required to remove it).
eff
It is important to bear in mind that when speaking about the location of electrons with
respect to the nucleus, we are talking about a probability (see Heisenberg’s uncer-
tainty principle). The actual effective nuclear charge is therefore in fluctuation due to
the location of an electron relative to the nucleus, and also due to electron-electron
repulsions. Any theorized effective nuclear charge is a kind of mean between larger
and smaller positive charges experienced during the path of an electron.
Practice
Find out what the effective nuclear charge would be for neon and sodium for the
electrons in each energy level.
a) What charge is felt by the electrons in the first level of a neon atom?
b) What charge is felt by the electrons in the second level (valence level) of a neon
atom?
c) What charge is felt by the electrons in the first level of a sodium atom?

African Virtual University 0
d) What charge is felt by the electrons in the second level of a sodium atom?
e) What charge is felt by the electrons in the third (valence) level of a sodium
atom?
Answers; a) 10, b) 8, c) 9, d) 1.
Problem set Unit 2 (accounts for 15 %).
1. Determine the number of valence electrons for the elements in group II:
a) 1,
b) 2,
c) 5
d) 8
2. What group or family of elements (IUPAC criteria) does silicon belong to?
a) 3,
b) 14,
c) IVA,
d) 4.
3. What is the name of the Group IIA elements?
a) alkali metals b) alkaline-earth metals c) halogens, d) Noble metals
4 . Which of the following is an inert gas?
a) hydrogen b) krypton
c) chlorine,
d) Nitrogen
5. In the Periodic Trends, which element has the smallest atomic radius?
a) Mg,
b) Ca,
c)Sr,
d) Be
6. What group of elements on the periodic table has the greatest atomic size?
a) The halogens b) The noble gases c)The alkali metals d) p-block elements
7. Which of the following sets are isoelectronic with each other? (T).
a) Rb+, Sr+2, Xe
b) Al+3, Na+, Ne
c) Br-, Na+, Se-2
8. Arrange the atoms and ions in order of increasing size, Rb+, Na+, and K+.
a) Na+ < K+ < Rb+
b) Rb+ < K+ < Na+
c) Na+ < Rb+ < K+

African Virtual University
9. Which is the electronic configuration of a H3 atom in the ground state?.
1
a) 1s1,
b) 1s2,
c) 1s22s1,
d) 1s22s2.
10. In which sub shell will the electrons have the highest energy?.
a) 3p,
b) 2p,
c) 3s,
d) 4s.
11. Which atom will form the most polar bond with hydrogen?.
a) F,
b) Cl,
c) Br,
d) I.
12. Which electron configuration represents the atom in the period 2 with the largest
covalent atomic radius
a) 1s22s1,
b) 1s12s2,
c) 1s22s22p1, d) 1s22s22p2
13. The elements of period 3 that has the highest ionization energy is;
a) a noble gas, b) an alkali metal, c) halogen, d) an alkali earth metal.
14. Magnessim has a smaller atomic radius than Sodium because the magnesium
atom has more,
a) Valency electrons, b) energy levels,
c) Protons,
d) neutrons.
15. As one proceeds from the left to the right across period 2, ionization energy
generally, a) decreases and atomic sizes also decrease, b) decrease and atomic
size increase, c) increase and atomic size decrease, d) increase and atomic size
increase.
Answer key
1..b, 2. b, 3. b, 4. b, 5. d, 6. c, 7. b, 8. a, 9.a, 10. d, 11.a, 12. d, 13. a, 14. c, 15. c.
.

African Virtual University
Learning activity # 3
Title of Learning Activity : GEnERAl PROPERTIES Of s And p BlOCK
ElEmEnTS
At the end of this Unit, the learner should be able to;
1. Predict the valency and oxidation states of the s-, and p-block elements
2. State the name(s) of simple s-, and p-block elements