The time to strike the ground is obtained by considering motion in vertical direction.
Here, uy = 0 and y=T (total time of flight)
Thus, we see that time of flight is independent of both mass and speed of the projectile in the
horizontal direction. The two balls, therefore, strike the ground simultaneously.
Hence, option (d) is correct.
Exercise 27.
A body dropped from a height "h" strikes the ground with a velocity 3 m/s. Another body of same
mass is projected horizontally from the same height with an initial speed of 4 m/s. The final
velocity of the second body (in m/s), when it strikes the earth will be :
We can use the fact that velocities in vertical direction, attained by two bodies through same
displacement, are equal. As such, velocity of the second body , on reaching the ground, would also







be 3 m/s. Now, there is no acceleration in horizontal direction. The horizontal component of
velocity of the second body, therefore, remains constant.
and
The resultant velocity of two component velocities in mutually perpendicular directions is :
Exercise 28.
A projectile (A) is dropped from a height and another projectile (B) is projected in horizontal
direction with a speed of 5 m/s from the same height. Then the correct statement(s) is(are) :
(a) The projectile (A) reach the ground earlier than projectile (B).
(b) Both projectiles reach the ground with the same speed.
(c) Both projectiles reach the ground simultaneously.
(d) The projectiles reach the ground with different speeds.
First three options pertain to the time of flight. The time of flight depends only the vertical
displacement and vertical component of projection velocity. The vertical components of
projection in both cases are zero. The time of flight (T) in either case is obtained by considering
motion in vertical direction as :
Hence, both projectiles reach the ground simultaneously. On the other hand, component of
velocity in vertical direction, on reaching the ground is :
vy = uy + ay ⇒ T = 0 + g T
Putting value of T, we have :
Projectile (A) has no component of velocity in horizontal direction, whereas projectile (B) has
finite component of velocity in horizontal direction. As such, velocities of projectiles and hence
the speeds of the particles on reaching the ground are different.
Hence, options (c) and (d) are correct.
Exercise 29.
Four projectiles, "A","B","C" and "D" are projected from top of a tower with velocities (in m/s) 10
i + 10 j, 10 i - 20 j , -10 i - 10 j and -20 i + 10 j in the coordinate system having point of projection as origin. If "x" and "y" coordinates are in horizontal and vertical directions
respectively, then :
(a)Time of flight of C is least.
(b) Time of flight of B is least.
(c) Times of flights of A and D are greatest.
(d) Times of flights of A and D are least.
The time of flight of a projectile solely depends on vertical component of velocity.
Figure 4.37. Projectile motion
Projectile motion
The projectile "A" is thrown up from an elevated point with vertical component of velocity 10
m/s. It travels to the maximum height ( H 1 ) and the elevation from the ground( H 2 ).
The projectile "B" is thrown down from an elevated point with vertical component of velocity 20
m/s. It travels only the elevation from the ground ( H 2 ).
The projectile "C" is thrown down from an elevated point with vertical component of velocity 10
m/s. It travels only the elevation from the ground ( H 2 ).
The projectile "D" is thrown up from an elevated point with vertical component of velocity 15
m/s. It travels to the maximum height ( H 1 ) and the elevation from the ground( H 2 ).
Clearly, projectile "B" and "C" travel the minimum vertical displacement. As vertical downward
component of velocity of "B" is greater than that of "C", the projectile "B" takes the least time.
The projectiles "A" and "D" are projected up with same vertical components of velocities i.e. 10
m/s and take same time to travel to reach the ground. As the projectiles are projected up, they take
more time than projectiles projected down.
Hence, options (b) and (c) are correct.
Acknowledgment
Author wishes to thank Scott Kravitz, Programming Assistant, Connexions for making suggestion
to remove syntax error in the module.
Projectile motion types (application)*
Questions and their answers are presented here in the module text format as if it were an extension
of the treatment of the topic. The idea is to provide a verbose explanation, detailing the
application of theory. Solution presented is, therefore, treated as the part of the understanding
process – not merely a Q/A session. The emphasis is to enforce ideas and concepts, which can not
be completely absorbed unless they are put to real time situation.
Hints on solving problems
1: Identify projectile motion types. The possible variants are :
Projectile is thrown in horizontal direction. In this case, initial vertical component of velocity
is zero. Consider horizontal direction as positive x-direction and vertically downward direction
as positive y-direction.
Projectile is thrown above horizontal level. The projectile first goes up and then comes down
below the level of projection
Projectile is thrown below horizontal level. Consider horizontal direction as positive x-
direction and vertically downward direction as positive y-direction.

2: We can not use standard equations of time of flight, maximum height and horizontal range. We
need to analyze the problem in vertical direction for time of flight and maximum height.
Remember that determination of horizontal range will involve analysis in both vertical (for time
of flight) and horizontal (for the horizontal range) directions.
3: However, if problem has information about motion in horizontal direction, then it is always
advantageous to analyze motion in horizontal direction.
Representative problems and their solutions
We discuss problems, which highlight certain aspects of the study leading to the projectile motion
types. The questions are categorized in terms of the characterizing features of the subject matter :
Time of flight
Range of flight
Initial velocity
Final velocity
Time of flight
Example 4.27.
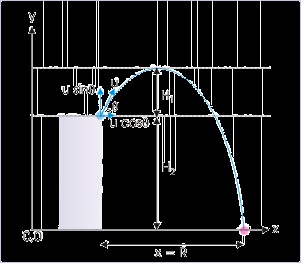
Problem : A ball from a tower of height 30 m is projected down at an angle of 30° from the
horizontal with a speed of 10 m/s. How long does ball take to reach the ground? (consider g =
10
)
Solution : Here, we consider a reference system whose origin coincides with the point of
projection. Further, we consider that the downward direction is positive y - direction.



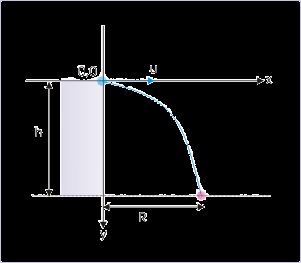



Figure 4.38. Projectile motion
Motion in vertical direction :
Here,
. Using
, we have :
Neglecting negative value of time, t = 2 s
Range of flight
Example 4.28.
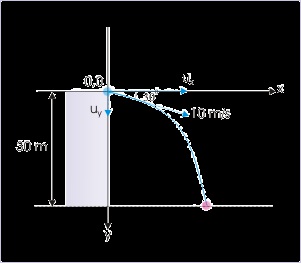
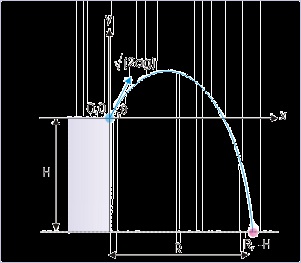
Problem : A ball is thrown from a tower of height “h” in the horizontal direction at a speed
“u”. Find the horizontal range of the projectile.
Solution : Here, we consider a reference system whose origin coincides with the point of
projection. we consider that the downward direction is positive y - direction.
Figure 4.39. Projectile motion
Motion in the vertical direction :
Here,
and t = T (total time of flight)
Putting expression of total time of flight in the expression for horizontal range, we have :

Example 4.29.
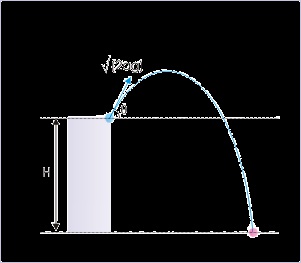
Problem : A projectile is projected up with a velocity √(2ag) at an angle “θ” from an
elevated position as shown in the figure. Find the maximum horizontal range that can be
achieved.
Figure 4.40. Projectile motion
Projectile projected from an elevated point .
Solution : In order to determine the maximum horizontal range, we need to find an expression
involving horizontal range. We shall use the equation of projectile as we have the final
coordinates of the motion as shown in the figure below :
Figure 4.41. Projectile motion
Projectile projected from an elevated point .







Substituting and changing trigonometric ratio with the objective to create a quadratic equation
in “tan θ” :
Rearranging, we have :
R 2 tan2 θ − 4 a R tan θ + ( R 2 − 4 a H ) = 0
For tan θ to be real, it is required that
16 a 2 R 2 ≥ 4 R 2 ( R 2 − 4 a H )
⇒ 4 a 2 ≥ ( R 2 − 4 a H )
⇒ R 2 ≤ 4 a ( a + H )
Hence, maximum possible range is :
Initial velocity
Example 4.30.
Problem : A ball is thrown horizontally from the top of the tower to hit the ground at an angle
of 45° in 2 s. Find the speed of the ball with which it was projected.
Solution : The question provides the angle at which the ball hits the ground. A hit at 45°
means that horizontal and vertical speeds are equal.
⇒ vx = vy
However, we know that horizontal component of velocity does not change with time. Hence,
final velocity in horizontal direction is same as initial velocity in that direction.
⇒ vx = vy = ux
We can now find the vertical component of velocity at the time projectile hits the ground by
considering motion in vertical direction. Here,
Using equation of motion in vertical direction, assuming downward direction as positive :





vy = uy + a t
Hence, the speed with which the ball was projected in horizontal direction is :
Final velocity
Example 4.31.
Problem : A ball “A” is thrown from the edge of building “h”, at an angle of 30° from the
horizontal, in upward direction. Another ball ”B” is thrown at the same speed from the same
position, making same angle with horizontal, in vertically downward direction. If "u" be the
speed of projection, then find their speed at the time of striking the ground.
Solution : The horizontal components of velocity for two projectiles are equal. Further,
horizontal component of velocity remains unaltered during projectile motion. The speed of the
projectile at the time of striking depends solely on vertical component of velocity. For the
shake of convenience of analysis, we consider point of projection as the origin of coordinate
system and vertically downward direction as positive y - direction.
Figure 4.42. Projectile motion
Motion in vertical direction :
For A,
For B,
Thus, velocities in vertical direction are equal in magnitude, but opposite in direction. The
ball,"A", which is thrown upward, returns after reaching the maximum vertical height. For
consideration in vertical direction, the ball returns to the point of projection with same speed






it was projected. What it means that the vertical component of velocity of ball "A" on return at
the point projection is "u/2". This further means that two balls "A" and "B", as a matter of fact, travel down with same downward vertical component of velocity.
In other words, the ball "A" returns to its initial position acquiring same speed "u/2" as that of
ball "B" before starting its downward journey. Thus, speeds of two balls are same i.e "u/2" for
downward motion. Hence, two balls strike the ground with same speed. Let the final speed is
"v".
Now, we apply equation of motion to determine the final speed in the vertical direction.
v 2 y = u 2 y + 2 g h
Putting values, we have :
The horizontal component of velocity remains same during the journey. It is given as :
The resultant of two mutually perpendicular components is obtained, using Pythagoras
theorem :
Projectile motion on an incline*
Projectile motion on an incline plane is one of the various projectile motion types. The main
distinguishing aspect is that points of projection and return are not on the same horizontal plane.
There are two possibilities : (i) the point of return is at a higher level than the point of projection
i.e projectile is thrown up the incline and (ii) Point of return is at a lower level than point of
projection i.e. projectile is thrown down the incline.
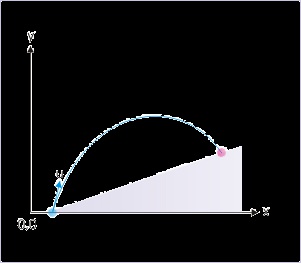
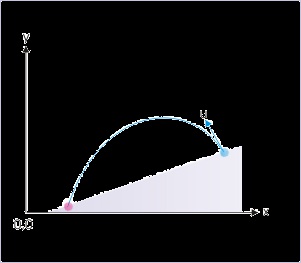
(a) Projection up the incline
(b) Projection down the incline
Figure 4.43. Projection on the incline
We have so far studied the projectile motion, using technique of component motions in two
mutually perpendicular directions – one which is horizontal and the other which is vertical. We
can simply extend the methodology to these types of projectile motion types as well.
Alternatively, we can choose coordinate axes along the incline and in the direction of
perpendicular to the incline. The analysis of projectile motion in two coordinate systems differs in
the detail of treatment.
For convenience of comparison, we shall refer projectile motion on a horizontal surface as the
“normal case”. The reference to “normal case” enables us to note differences and similarities
between “normal case” and the case of projectile motion on an incline plane.
Analyzing alternatives
As pointed out, there are two different approaches of analyzing projectile motion on an incline
plane. The first approach could be to continue analyzing motion in two mutually perpendicular
horizontal and vertical directions. The second approach could be to analyze motion by changing
the reference orientation i.e. we set up our coordinate system along the incline and a direction
along the perpendicular to incline.
The analysis alternatives are, therefore, distinguished on the basis of coordinate system that we
choose to employ :
planar coordinates along incline (x) and perpendicular to incline (y)
planar coordinates in horizontal (x) and vertical (y) directions

(a) With reference to incline
(b) With reference to horizontal
Figure 4.44. Coordinate systems
The two alternatives, as a matter of fact, are entirely equivalent. However, we shall study both
alternatives separately for the simple reason that they provide advantage in analyzing projectile
motion in specific situation.
Projection up the incline
As pointed out, the projection up the incline can be studied in two alternative ways. We discuss
each of the approach, highlighting intricacies of each approach in the following sub-section.
Coordinates along incline (x) and perpendicular to incline (y)
This approach is typically superior approach in so far as it renders measurement of time of flight
in a relatively simpler manner. However, before we proceed to analyze projectile motion in this
new coordinate set up, we need to identify and understand attributes of motion in mutually
perpendicular directions.
Measurement of angle of projection is one attribute that needs to be handled in a consistent
manner. It is always convenient to follow certain convention in referring angles involved. We had
earlier denoted the angle of projection as measured from the horizontal and denoted the same by
the symbol “θ”. It is evident that it would be reasonable to extend the same convention and also
retain the same symbol for the angle of projection.
It also follows that we measure other angles from the horizontal – even if we select x-coordinate
in any other direction like along the incline. This convention avoids confusion. For example, the
angle of incline “α” is measured from the horizontal. The horizontal reference, therefore, is
actually a general reference for measurement of angles in the study of projectile motion.
Now, let us have a look at other characterizing aspects of new analysis set up :

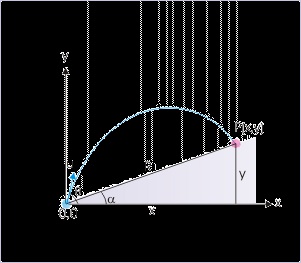
1: The coordinate “x” is along the incline – not in the horizontal direction; and the coordinate “y”
is perpendicular to incline – not in the vertical direction.
2: Angle with the incline
From the figure, it is clear that the angle that the velocity of projection makes with x-axis (i.e.
incline) is “θ – α”.
Figure 4.45. Projectile motion up an incline
The projection from lower level.
3: The point of return
The point of return is specified by the coordinate R,0 in the coordinate system, where “R” is the
range along the incline.
4: Components of initial velocity
ux = u cos ( θ − α )
uy = u sin ( θ − α )
5: The components of acceleration
In order to determine the components of acceleration in new coordinate directions, we need to
know the angle between acceleration due to gravity and y-axis. We see that the direction of
acceleration is perpendicular to the base of incline (i.e. horizontal) and y-axis is perpendicular to
the incline.
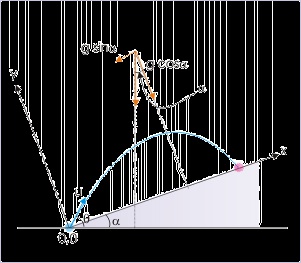
Figure 4.46. Components of acceleration due to gravity
The acceleration due to gravity forms an angle with y-axis, which is equal to angle of incline.
Thus, the angle between acceleration due to gravity and y – axis is equal to the angle of incline i.e.
“α”. Therefore, components of acceleration due to gravity are :
ax = − g sin α
ay = – g cos α
The negative signs precede the expression as two components are in the opposite directions to the
positive directions of the coordinates.
6: Unlike in the normal case, the motion in x-direction i.e. along the incline is not uniform
motion, but a decelerated motion. The velocity is in positive x-direction, whereas acceleration is
in negative x-direction. As such, component of motion in x-direction is decelerated at a constant
rate “gsin α”.
Time of flight
The time of flight (T) is obtained by analyzing motion in y-direction (which is no more vertical as
in the normal case). The displacement in y-direction after the projectile has returned to the
incline, however, is zero as in the normal case. Thus,








Figure 4.47. Projectile motion up an incline
<























































