⇒ 0 = u 2 − 2 g H
In order to answer this question, we need to identify the velocity with which projectile
rebounds. Since impact is considered elastic, the projectile is rebounded without any loss of
speed. The projectile is rebounded such that angle of incidence i.e. the angle with the normal
is equal to angle of reflection.
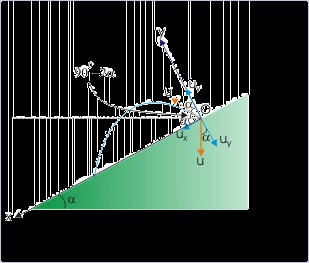
Figure 4.63. Projectile motion on an incline
The ball impacts incline elastically.
The components of velocity along the incline and perpendicular to it are shown in the figure.
The motion of ball, thereafter, is same as that of a projectile over an incline. Here, we shall
analyze motion in y-direction (normal to the incline) to find the time of flight. We note that
the net displacement between two strikes is zero in y – direction.
Applying equation of motion
T = 0
Or




Putting value of initial speed in the equation of time of flight, we have :
It should be noted here that we can find the time of flight also by using standard formula of
time of flight for projectile motion down the incline. The time of flight for projection down an
incline is given as :
We need to be careful while appropriating angles in the above expression. It may be recalled
that all angles are measured from the horizontal. We redraw the figure to denote the value of
angle of projection “θ” from the horizon.
Figure 4.64. Projectile motion on an incline
The ball impacts incline elastically.
Projectile motion on two inclines
Example 4.39.
Problem : Two incline plane of angles 30° and 60° are placed touching each other at the base
as shown in the figure. A projectile is projected at right angle with a speed of 10√3 m/s from
point “P” and hits the other incline at point “Q” normally. Find the linear distance between
PQ.
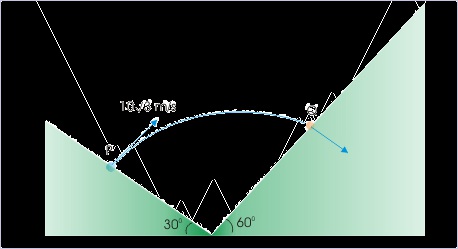
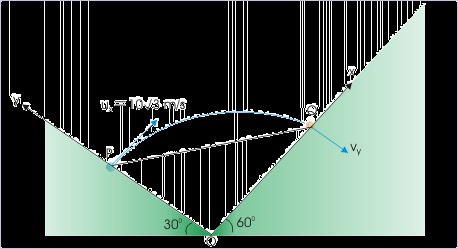


Figure 4.65. Projectile motion on two inclines
A projectile projected at right angle from an incline hits another incline at right angle.
Solution : We notice here OPQ forms a right angle triangle at “O”. The linear distance, “PQ”
is related as :
Figure 4.66. Projectile motion on two inclines
A projectile projected at right angle from an incline hits another incline at right angle.
P Q 2 = O P 2 + O Q 2
In order to find “PQ”, we need to know “OP” and “OQ”. We can find “OP”, considering
motion in y-direction.
Similarly,
In order to evaluate these two relations, we need to find components of accelerations and time
of flight.
Considering first incline, we have :








In order to find the time of flight, we can further use the fact that the component of velocity in
x-direction i.e. along the second incline is zero. This, in turn, suggests that we can analyze
motion in x-direction to obtain time of flight.
In x-direction,
vx = ux + ax T
⇒ 0 = ux + ax T
Putting values in the equation and solving, we have :
Now, we can evaluate “x” and “y” displacements as :
Considering positive values, the linear distance, “PQ” is given as :
Relative motion of projectiles*
In this module, we shall apply the concept of relative velocity and relative acceleration to the
projectile motion. The description here is essentially same as the analysis of relative motion in
two dimensions, which was described earlier in the course except that there is emphasis on
projectile motion. Besides, we shall extend the concept of relative motion to analyze the
possibility of collision between projectiles.
We shall maintain the convention of subscript designation for relative quantities for the sake of
continuity. The first letter of the subscript determines the “object”, whereas the second letter
determines the “other object” with respect to which measurement is carried out. Some expansion
of meaning is given here to quickly recapitulate uses of subscripted terms :
v AB : Relative velocity of object “A” with respect to object “B”
vABx : Component of relative velocity of object “A” with respect to object “B” in x-direction

For two dimensional case, the relative velocity is denoted with bold type vector symbol. We shall
, however, favor use of component scalar symbol with appropriate sign to represent velocity
vector in two dimensions like in the component direction along the axes of the coordinate system.
The generic expression for two dimensional relative velocity are :
In vector notation :
()
v AB = v A − v B
In component scalar form :
()
vABx = vAx – vBx
()
vABy = vAy – vBy
Relative velocity of projectiles
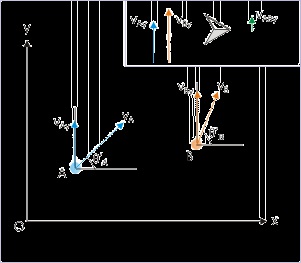
The relative velocity of projectiles can be found out, if we have the expressions of velocities of
the two projectiles at a given time. Let “ v A ” and “ v B ” denote velocities of two projectiles respectively at a given instant “t”. Then :
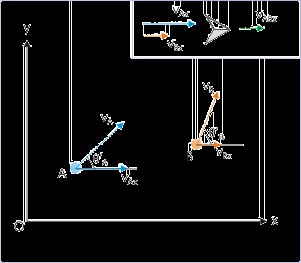
Figure 4.67. Relative velocity of projectiles
Velocities of projectiles.
v A = vAx i + vAy j
v B = vBx i + vBy j
Hence, relative velocity of projectile “A” with respect to projectile “B” is :
v AB = v A – v B = vAx i + vAy j − vBx i − vBy j

()
v AB = ( vAx − vBx ) i + ( vAy − vBy ) j We can interpret this expression of relative velocity as equivalent to consideration of relative
velocity in component directions. In the nutshell, it means that we can determine relative velocity
in two mutually perpendicular directions and then combine them as vector sum to obtain the
resultant relative velocity. Mathematically,
()
v AB = vABx i + vABy j
where,
vABx = vAx − vBx
This is a significant analysis simplification as study of relative motion in one dimension can be
done with scalar representation with appropriate sign.
Interpretation of relative velocity of projectiles
The interpretation is best understood in terms of component relative motions. We consider motion
in both horizontal and vertical directions.
Relative velocity in horizontal direction
The interpretation is best understood in terms of component relative motion. In horizontal
direction, the motion is uniform for both projectiles. It follows then that relative velocity in
horizontal x-direction is also a uniform velocity i.e. motion without acceleration.
Figure 4.68. Component relative velocity
Component relative velocity in x-direction.
The relative velocity in x-direction is :
vABx = vAx − vBx
As horizontal component of velocity of projectile does not change with time, we can re-write the
equation of component relative velocity as :
()
vABx = uAx − uBx
Significantly, relative velocity in x-direction is determined by the initial velocities or initial
conditions of the projection of two projectiles. It is expected also as components of velocities in
x-direction do not change with time. The initial velocity, on the other hand, is fixed for a given
projectile motion. As such, horizontal component of relative velocity is constant. A plot of
relative velocity in x - direction .vs. time will be a straight line parallel to time axis.
The separation between two objects in x-direction at a given time "t" depends on two factors : (i)
the initial separation of two objects in x-direction and (ii) relative velocity in x - direction. The
separation in x - direction is given as :
Δ x = xA − xB = x 0 + vABx t
where x 0 is the initial separation between two projectiles in x-direction. Clearly, the separation in
horizontal direction .vs. time plot would be a straight line with a constant slope. In physical terms,
the separation between two projectiles in horizontal direction keeps increasing at a constant rate,
which is equal to the magnitude of the component of relative velocity in that direction.
Relative velocity in vertical direction
The motion in the vertical direction, however, is subject to acceleration due to gravity, which
always acts in vertically downward direction. The relative velocity in y-direction is :
Figure 4.69. Component relative velocity
Component relative velocity in y-direction.
vABy = vAy − vBy
As vertical component of motion is not a uniform motion, we can use equation of motion to
determine velocity at a given time “t” as,
vAy = uAy − g t
vBy = uBy − g t
Putting in the expression of relative velocity in y-direction, we have :
vABy = vAy − vBy = uAy − g t − uBy + g t ()
⇒ vABy = uAy − uBy
The important aspect of the relative velocity in vertical y-direction is that acceleration due to
gravity has not made any difference. The component relative velocity in y-direction is equal to
simple difference of components of initial velocities of two projectiles in vertical direction. It is
clearly due to the fact the acceleration of two projectiles in y-direction are same i.e. acceleration
due to gravity and hence relative acceleration between two projectiles in vertical direction is zero.
It means that the nature of relative velocity in vertical direction is same as that in the horizontal
direction. A plot of relative velocity in y -direction .vs. time will be a straight line parallel to time
axis.
The separation between two objects in y-direction at a given time "t" depends on two factors : (i)
the initial separation of two objects in y-direction and (ii) relative velocity in y - direction. The
separation in y - direction is given as :
Δ y = yA − yB = y 0 + vABy t
where y 0 is the initial separation between two projectiles in y-direction. Note that acceleration
term has not appeared in the expression of relative velocity, because they cancel out. Clearly, the
separation in vertical direction .vs. time plot would be a straight line with a constant slope. In
physical terms, the separation between two projectiles in vertical direction keeps increasing at a
constant rate, which is equal to the magnitude of the component of relative velocity in that
direction.
Resultant relative motion
The component relative velocities in two mutually perpendicular directions have been derived in
the previous section as :
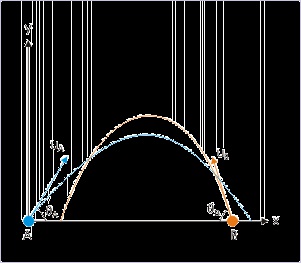
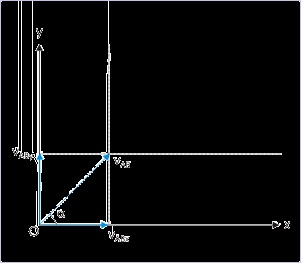
Figure 4.70. Relative velocity of projectiles
Relative velocity of projectiles depends on initial velocities of projectiles.
vABx = uAx − uBx
vABy = uAy − uBy
These equations are very important results. It means that relative velocity between projectiles is
exclusively determined by initial velocities of the two projectiles i.e. by the initial conditions of
the two projectiles as shown in the figure below. The component relative velocities do not depend
on the subsequent motion i.e. velocities. The resultant relative velocity is vector sum of
component relative velocities :
v AB = vABx i + vABy j
Figure 4.71. Resultant relative velocity of projectiles
Resultant relative velocity of projectiles is constant.
Since the component relative velocities do not depend on the subsequent motion, the resultant
relative velocity also does not depend on the subsequent motion. The magnitude of resultant







relative velocity is given by :
()
The slope of the relative velocity of “A” with respect to “B” from x-direction is given as :
()
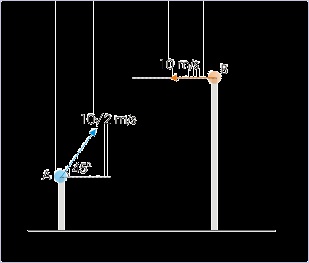
Example 4.40.
Problem : Two projectiles are projected simultaneously from two towers as shown in the
figure. Find the magnitude of relative velocity, vAB , and the angle that relative velocity makes
with horizontal direction
Figure 4.72. Relative motion of projectiles
Relative motion of projectiles
Solution : We shall first calculate relative velocity in horizontal and vertical directions and
then combine them to find the resultant relative velocity. Let "x" and "y" axes be in horizontal
and perpendicular directions. In x-direction,
In y-direction,
The magnitude of relative velocity is :
The angle that relative velocity makes with horizontal is :
Physical interpretation of relative velocity of projectiles
The physical interpretation of the results obtained in the previous section will help us to
understand relative motion between two projectiles. We recall that relative velocity can be
interpreted by assuming that the reference object is stationary. Consider the expression, for
example,
vABx = uAx − uBx
What it means that relative velocity “vABx” of object “A” with respect to object “B” in x-
direction is the velocity of the object “A” in x-direction as seen by the stationary object “B”. This
interpretation helps us in understanding the nature of relative velocity of projectiles.
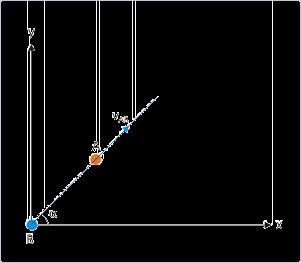
Extending the reasoning, we can say that object “A” is moving with uniform motion in “x” and
“y” directions as seen by the stationary object “B”. The resultant motion of “A”, therefore, is
along a straight line with a constant slope. This result may be a bit surprising as we might have
expected that two projectiles see (if they could) each other moving along some curve - not a
straight line.
Figure 4.73. Relative velocity of projectiles
Relative velocity of projectiles is constant.
Special cases
There are two interesting cases. What if horizontal component of velocities of the two projectiles
are same? In this case, relative velocity of projectiles in horizontal direction is zero. Also, it is
imperative that there is no change in the initial separation between two projectiles in x-direction.
Mathematically,
vABx = uAx – uBx = 0
There is no relative motion between two projectiles in horizontal direction. They may, however,
move with respect to each other in y-direction. The relative velocity in y-direction is given by :
vABy = uAy − uBy
Since relative velocity in x-direction is zero, the relative velocity in y-direction is also the net
relative velocity between two projectiles.
In the second case, components of velocities in y-direction are equal. In this case, there is no
relative velocity in y-direction. The projectiles may, however, have relative velocity in x-
direction. As such the relative velocity in y-direction is also the net relative velocity between two
projectiles.
Exercises
Exercise 38.
Two projectiles are projected simultaneously at same speeds, but with different angles of
projections from a common point in a given vertical plane. The path of one projectile, as viewed
from other projectile is :
(a) a straight line parallel to horizontal
(b) a straight line parallel to vertical
(c) a circle
(d) None of above
The component relative velocities in horizontal and vertical directions are, defined in terms of
initial velocities, which are constant for the given pair of projectiles. Therefore, the relative
velocities of two projectiles in horizontal and vertical directions are constants. Let " uA ” and “
uB ” be the initial velocities of two projectiles, then component relative velocities in "x" and "y"
directions are :

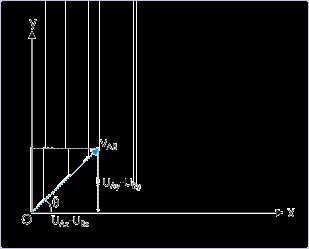

Figure 4.73. Relative motion of projectiles
Relative motion of projectiles
vABx = uAx − uBx vABy = uAy − uBy
The resultant relative velocity is :
u AB = ( uAx − uBx ) i + ( uAy − uBy ) j As given in the question, the initial speeds of the projectiles are same, but angles of projections
are different. Since sine and cosine of two different angles are different, it follows that component
velocities of two projectiles are different in either direction. This is ensured as speeds of two
projectiles are same. It implies that components (horizontal or vertical) of the relative velocity
are non-zero and finite constant. The resultant relative velocity is, thus, constant, making an angle
" θ " with horizontal (x-axis) such that :
Figure 4.73. Relative motion of projectiles
Relative motion of projectiles
Thus, one projectile (B) sees other projectile (A) moving in a straight line with constant velocity,
which makes a constant angle with the horizontal. Hence, option (d) is correct.
Exercise 39.
Two projectiles are projected simultaneously at different velocities from a common point in a
given vertical plane. If the components of initial velocities of two projectiles in horizontal
direction are equal, then the path of one projectile as viewed from other projectile is :
(a) a straight line parallel to horizontal
(b) a straight line parallel to vertical
(c) a parabola
(d) None of above
The component






































