Hence, options (b) and (d) are correct.
Exercise 49.
A particle executes uniform circular motion with a speed “v” in xy plane, starting from position
(r,0), where “r” denotes the radius of the circle. Then
(a) the component of velocity along x - axis is constant
(b) the component of acceleration along x - axis is constant
(c) the angle swept by the line joining center and particle in equal time interval is constant
(d) the velocity is parallel to external force on the particle
The component of velocity along x - direction is “-v sinθ” and is not a constant. The component of
acceleration along x - direction is “
” and is not a constant. The external force in
uniform circular motion is equal to centripetal force, which is directed towards the center. Thus,
the velocity is perpendicular to external force.
On the other hand, the particle covers equal circular arc in equal time interval. Hence, the angle
subtended by the arc at the center is also equal in equal time interval.
Hence, option (c) is correct.
Exercise 50.
A particle executes uniform circular motion with a speed “v” in anticlockwise direction, starting
from position (r,0), where “r” denotes the radius of the circle. Then, both components of the
velocities are positive in :
(a) first quadrant of the motion
(b) second quadrant of the motion
(c) third quadrant of the motion
(d) fourth quadrant of the motion
From the figure, it is clear that the components of velocity in the fourth quadrant are both
positive.
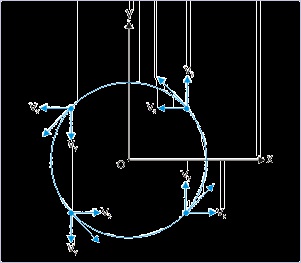




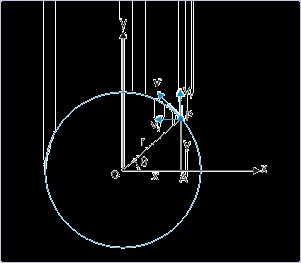

Figure 4.90. Uniform circular motion
Hence, option (d) is correct.
Exercise 51.
A particle executes uniform circular motion with a constant speed of 1 m/s in xy - plane. The
particle starts moving with constant speed from position (r,0), where "r" denotes the radius of the
circle. If center of circle is the origin of the coordinate system, then what is the velocity in "m/s"
of the particle at the position specified by the coordinates (3m,-4m) ?
(a)
(b)
(c)
(d)
Here, the inputs are given in terms of coordinates. Thus, we shall use the expression of velocity,
which involves coordinates. Velocity of the particle in circular motion is given by :
Figure 4.90. Uniform circular motion



Here, radius of the circle is :
Hence, option (a) is correct.
Uniform circular motion (application)*
Questions and their answers are presented here in the module text format as if it were an extension
of the treatment of the topic. The idea is to provide a verbose explanation, detailing the
application of theory. Solution presented is, therefore, treated as the part of the understanding
process – not merely a Q/A session. The emphasis is to enforce ideas and concepts, which can not
be completely absorbed unless they are put to real time situation.
Representative problems and their solutions
We discuss problems, which highlight certain aspects of the study leading to the uniform circular
motion. The questions are categorized in terms of the characterizing features of the subject matter
:
Direction of velocity
Direction of position vector
Velocity
Relative speed
Nature of UCM
Direction of velocity
Example 4.47.
Problem : A particle moves in xy-plane along a circle of radius "r". The particle moves at a
constant speed in anti-clockwise direction with center of circle as the origin of the coordinate
system. At a certain instant, the velocity of the particle is i – √3 j. Determine the angle that

velocity makes with x-direction.
Solution : The sign of y-component of velocity is negative, whereas that of x-component of
velocity is positive. It means that the particle is in the third quadrant of the circle as shown in
the figure.
Figure 4.91. Top view of uniform circular motion in xy-plane
The acute angle formed by the velocity with x-axis is obtained by considering the magnitude
of components (without sign) as :
⇒ α = 600
This is the required angle as measured in clockwise direction from x-axis. If the angle is
measured in anti-clockwise direction from positive direction of x-axis, then
⇒ α ′ = 3600 − 600 = 3000
Direction of position vector
Example 4.48.
Problem : A particle moves in xy-plane along a circle of radius “r”. The particle moves at a
constant speed in anti-clockwise direction with center of circle as the origin of the coordinate
system. At a certain instant, the velocity of the particle is i – √3 j. Determine the angle that
position vector makes with x-direction.
Solution : The sign of y-component of velocity is negative, whereas that of x-component of
velocity is positive. It means that the particle is in the third quadrant of the circle as shown in
the figure.
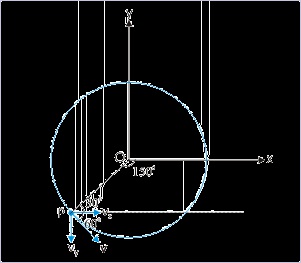


Figure 4.92. Top view of uniform circular motion in xy-plane
The acute angle formed by the velocity with x-axis is obtained by considering the magnitude
of components (without sign) as :
⇒ α = 600
But, we know that position vector is perpendicular to velocity vector. By geometry,
θ = 1800 − 300 = 1500
This is the angle as measured in clockwise direction from x-axis. If the angle is measured in
anti-clockwise direction from positive direction of x-axis, then
⇒ α ′ = 3600 − 1500 = 2100
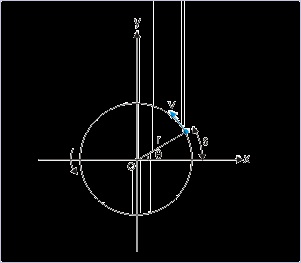
Note : Recall the derivation of the expression of velocity vector in the previous module. We
had denoted “θ” as the angle that position vector makes with x-axis (not the velocity vector).
See the figure that we had used to derive the velocity expression.
Figure 4.93. Top view of uniform circular motion in xy-plane




As a matter of fact “θ” is the angle that velocity vector makes with y-axis (not x-axis). We can
determine the angle “θ” by considering the sign while evaluating tan θ,
θ = 1500
Velocity
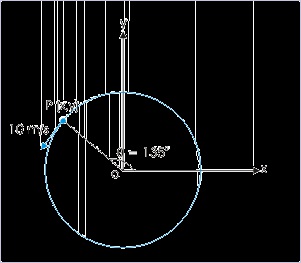
Example 4.49.
Problem : A particle moves with a speed 10 m/s in xy-plane along a circle of radius 10 m in
anti-clockwise direction. The particle starts moving with constant speed from position (r,0),
where "r" denotes the radius of the circle. Find the velocity of the particle (in m/s), when its
position makes an angle 135° with x – axis.
Solution : The velocity of the particle making an angle "θ" with x – axis is given as :
Figure 4.94. Uniform circular motion
Here,
Here, both the components are negative.






Relative speed
Example 4.50.
Problem : Two particles tracing a circle of radius 10 m begin their journey simultaneously
from a point on the circle in opposite directions. If their speeds are 2.0 m/s and 1.14 m/s
respectively, then find the time after which they collide.
Solution : The particles approach each other with a relative speed, which is equal to the sum
of their speeds.
For collision to take place, the particles need to cover the initial separation with the relative
speed as measured above. The time for collision is, thus, obtained as :
Nature of UCM
Example 4.51.
Problem : Two particles “A” and “B” are moving along circles of radii " rA " and " rB "
respectively at constant speeds. If the particles complete one revolution in same time, then
prove that speed of the particle is directly proportional to radius of the circular path.
Solution : As the time period of the UCM is same,
Hence, speed of the particle is directly proportional to the radius of the circle.
Example 4.52.
Problem : Two particles “A” and “B” are moving along circles of radii " rA " and " rB "
respectively at constant speeds. If the particles have same acceleration, then prove that speed
of the particle is directly proportional to square root of the radius of the circular path.
Solution : As the acceleration of the UCM is same,


Hence, speed of the particle is directly proportional to square root of the radius of the circular
path.
Circular motion and rotational kinematics*
In pure rotational motion, the constituent particles of a rigid body rotate about a fixed axis in a
circular trajectory. The particles, composing the rigid body, are always at a constant perpendicular
distance from the axis of rotation as their internal distances within the rigid body is locked.
Farther the particle from the axis of rotation, greater is the speed of rotation of the particle.
Clearly, rotation of a rigid body comprises of circular motion of individual particles.
Figure 4.95. Rotation of a rigid body about a fixed axis
Each particle constituting the body executes an uniform circular motion about the fixed axis.
We shall study these and other details about the rotational motion of rigid bodies at a later stage.
For now, we confine ourselves to the aspects of rotational motion, which are connected to the
circular motion as executed by a particle. In this background, we can say that uniform circular
motion (UCM) represents the basic form of circular motion and circular motion, in turn,
constitutes rotational motion of a rigid body.
The description of a circular and hence that of rotational motion is best suited to corresponding
angular quantities as against linear quantities that we have so far used to describe translational
motion. In this module, we shall introduce these angular quantities and prepare the ground work to
enable us apply the concepts of angular quantities to “circular motion” in general and “uniform
circulation motion” in particular.
Most important aspect of angular description as against linear description is that there exists one
to one correspondence of quantities describing motion : angular displacement (linear
displacement), angular velocity (linear velocity) and angular acceleration (linear acceleration).
Angular quantities
In this section, we discuss some of the defining quantities, which are used to study uniform
circular motion of a particle and rotational motion of rigid bodies. These quantities are angular
position, angular displacement and angular velocity. They possess directional properties. Their
measurement in counter clockwise direction is considered positive, whereas quantities measured
in clockwise direction is considered negative. This gives us a simplified scheme to represent an
angular vector by a simple variable, whose sign indicates its direction.
Notably, we shall not discuss angular acceleration in this module. It will be discussed as a part of
non-uniform circular motion in a separate module.
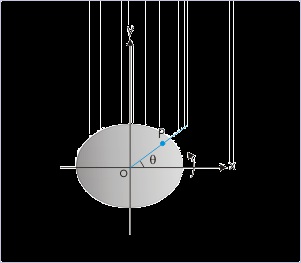
Angular position (θ)
We need two straight lines to measure an angle. In rotational motion, one of them represents fixed
direction, while another represents the rotating arm containing the particle. Both these lines are
perpendicular to the rotating axis. The rotating arm, additionally, passes through the position of
the particle.
Figure 4.96. Angular position (θ)
Angular position is the angle between reference direction and rotating arm.
For convenience, the reference direction like x – axis of the coordinate system serves to represent
fixed direction. The angle between reference direction and rotating arm (OP) at any instant is the
angular position of the particle (θ).
It must be clearly understood that angular position (θ) is an angle and does not represent the

position of the particle by itself. It requires to be paired with radius of the circle (r) along which
particle moves in order to specify the position of the particle. Thus, a specification of a position in
the reference system will require both “r” and “θ” to be specified.
Figure 4.97. Relation between distance (s) and angle (θ)
By geometry,
()
where "s" is the length of the arc subtending angle “θ” at the origin and “r” is the radius of the
circle containing the position of the particle. The angular position is measured in “radian”, which
has no dimension, being ratio of two lengths. One revolution contains 2π radians. The unit of
radian is related to other angle measuring units "degree" and "revolution" as :
1 revolution = 360° = 2π radian
The quantities related to angular motion are expressed in terms of angular position. It must be
ensured that values of angular position wherever it appears in the expression be substituted in
radians only. If the given value is in some other unit, then we first need to change the value
into radian. It is so because, radian is a unit derived from the definition of the angle. The
defining relation θ = s/r will not hold unless “θ” is in radian.
Angular displacement (Δθ)
Angular displacement is equal to the difference of angular positions at two instants of rotational
motion.
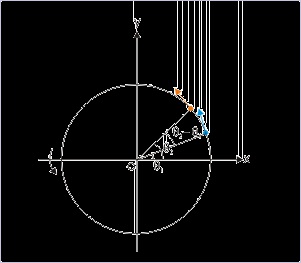



Figure 4.98. Angular displacement (Δθ)
Angular displacement is equal to the difference of angular positions at two positions.
()
The angular displacement is also measured in “radian” like angular position. In case our
measurement of angular position coincides with the reference direction, we can make substitution
as given here :
θ 1 = 0
θ 2 = θ
With these substitution, we can simply express angular displacement in terms of angle as :
⇒ Δ θ = θ 2 − θ 1 = θ − 0 = θ
Angular velocity (ω)
Angular speed is the ratio of the magnitude of angular displacement and time interval.
()
This ratio is called average angular velocity, when it is evaluated for finite time interval; and
instantaneous angular velocity, when it is evaluated for infinitesimally small period (Δ→0).
()
The angular velocity is measured in “rad/s”.
Description of circular motion






Circular motion is completely described when angular position of a particle is given as a function
of time like :
For example, θ = 2 t 2 – 3 t + 1 tells us the position of the particle with the progress of time. The attributes of circular motion such as angular velocity and acceleration are first and second time
derivatives of this function in time. Similarity to pure translational motion is quite obvious here.
In pure translational motion, each particle constituting a rigid body follows parallel linear paths.
The position of a particle is a function of time, whereby :
Example 4.53.
Problem : The angular position (in radian) of a particle under circular motion about a
perpendicular axis with respect to reference direction is given by the function in time
(seconds) as :
Find (i) angular position when angular velocity is zero and (ii) determine whether rotation is
clock-wise or anti-clockwise.
Solution : The angular velocity is equal to first derivative of angular position,
For ω= 0, we have :
The angular position at t = 0.1 s,
As the particle makes a positive angle with respect to reference direction, we conclude that the
particle is moving in anti-clockwise direction (We shall discuss the convention regarding
direction of angular quantities in detail subsequently).
Relationship between linear (v) and angular speed (ω)
In order to understand the relation, let us consider two uniform circular motions with equal time
period (T) along two circular trajectories of radii r 1 and r 2 ( r 2 > r 2 ). It is evident that particle along the outer circle is moving at a greater speed as it has to cover greater perimeter or distance.
On the other hand angular speeds of the two particles are equal as they transverse equal angles in a










given time.
This observation is key to understand the relation between linear and angular speed. Now, we
know that :
Differentiating with respect to time, we have :
Since, “r” is constant for a given circular motion,
.
Now,
is equal to linear speed, v. Hence,
()
This is the relation between angular and linear speeds. Though it is apparent, but it is emphasized
here for clarity that angular and linear speeds do not represent two separate individual speeds.
Remember that a particle can have only one speed at a particular point of time. They are, as a
matter of fact, equivalent representation of the same change of position with respect to time. They
represent same speed – but in different language or notation.
Example 4.54.
Problem : The angular position (in radian) of a particle with respect to reference direction,
along a circle of radius 0.5 m is given by the function in time (seconds) as :
Find linear velocity of the particle at t = 0 second.
Solution : The angular velocity is given by :
For t = 0, the angular velocity is :
The linear velocity at this instant is :
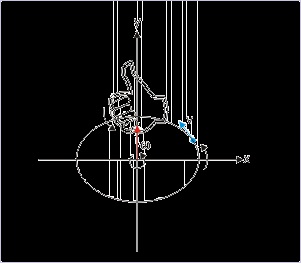
Vector representation of angular quantities
The angular quantities (displacement, velocity and acceleration) are also vector quantities like
their linear counter parts and follow vector rules of addition and multiplication, with the notable
exception of angular displacement. Angular displacement does not follow the rule of vector
addition strictly. In particular, it can be shown that addition of angular displacement depends on
the order in which they are added. This is contrary to the property of vector addition. Order of
addition should not affect the result. We intend here to skip the details of this exception to focus
on the subject matter in hand. Besides, we should know that we may completely ignore this
exception if the angles involved have small values.
The vector angular quantities like angular velocity ( ω) or ω (as scalar representation of angular
vector) is represented by a vector, whose direction is obtained by applying “Right hand rule”. We
just hold the axis of rotation with right hand in such a manner that the direction of the curl of
fingers is along the direction of the rotation. The direction of extended thumb (along y-axis in the
figure below) then represents the direction of angular velocity ( ω).
Figure 4.99. Vector cross product
Right Hand Rule (RHR)
The important aspect of angular vector representation is that the angular vector is essentially a
straight line of certain magnitude represented on certain scale with an arrow showing direction
(shown in the figure as a red line with arrow) – not a curl as some might have expected. Further,
the angular vector quantities are axial in nature. This means that they apply along the axis of
rotation. Now, there are only two possible directions along the axis of r
























































