our real time experience, we may substantiate this assertion. For example, we can deflect a foot
ball, applying force as we wish (in both magnitude and direction). The motion of the ball has no
bearing on how we apply force. Simply put : the magnitude and direction of the force (and that of
acceleration) is not dependent on the magnitude and direction of the velocity of the body.
In the nutshell, we conclude that force and hence acceleration is independent of the velocity of
the body. The magnitude and direction of the acceleration is determined by the magnitude and
direction of the force and mass of the body. This is an important clarification.
To elucidate the assertion further, let us consider parabolic motion of a ball as shown in the figure.
The important aspect of the parabolic motion is that the acceleration associated with motion is
simply ‘g’ as there is no other force present except the force of gravity. The resultant force and
mass of the ball together determine acceleration of the ball.
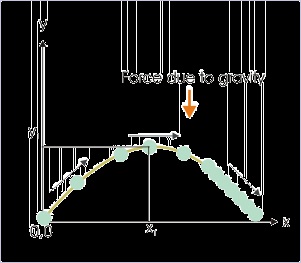
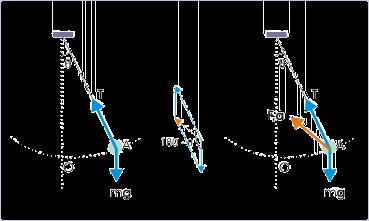

Figure 2.5. Parabolic motion
The resultant force and mass of the ball together determine acceleration of the ball
Example 2.2. Acceleration
Problem : If the tension in the string is T, when the string makes an angle θ with the vertical.
Find the acceleration of a pendulum bob, having a mass “m”.
Solution : As pointed out in our discussion, we need not study or consider velocities of bob to
get the answer. Instead we should strive to know the resultant force to find out acceleration,
using Newton’s second law of motion.
The forces, acting on the bob, are (i) force of gravity, mg, acting in the downward direction
and (ii) Tension, T, acting along the string. Hence, the acceleration of the bob is determined
by the resultant force, arising from the two forces.
Figure 2.6. Acceleration of a pendulum bob
Using parallelogram theorem for vector addition, the resultant force is :
The acceleration is in the direction of force as shown in the figure, whereas the magnitude of
the acceleration, a, is given by :

External force and possible scenarios
The change in velocity, resulting from the application of external force, may occur in magnitude
or direction or both.
1: When force is applied in a given direction and the object is stationary.
Under this situation, the magnitude of velocity increases with time, while the body follows a
linear path in the direction of force (or acceleration).
2: When force is applied in the direction of the motion, then it increases the magnitude of the
velocity without any change in the direction.
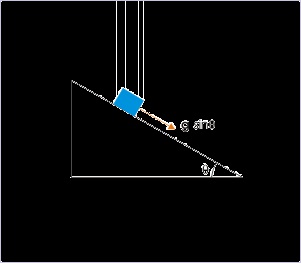
Let us consider a block sliding on a smooth incline surface as shown in the figure. The component
of the force due to gravity applies in the direction of motion. Under this situation, the magnitude
of velocity increases with time, while the body follows a linear path. There is no change in the
direction of motion.
Figure 2.7. A block sliding along smooth incline
The block moves faster as it moves down the slope
3: When force is applied in the opposite direction to the motion, then it decreases the magnitude
of the velocity without any change in the direction.
Take the example of a ball thrown vertically in the upward direction with certain velocity. Here,
force due to gravity is acting downwards. The ball linearly rises to the maximum height till the
velocity of ball reduces to zero.
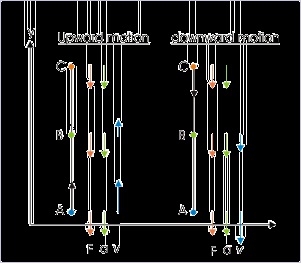

Figure 2.8. A ball thrown in vertical direction
The ball reverses its direction during motion.
During upward motion, we see that the force acts in the opposite direction to that of the velocity.
Under this situation, the magnitude of velocity decreases with time, while the body follows a
linear path. There is no change in the direction of motion.
The velocity of the object at the point, where motion changes direction, is zero and force is acting
downwards. This situation is same as the case 1. The object is at rest. Hence, object moves in the
direction of force i.e. in the downward direction.
In the figure above, the vectors drawn at various points represent the direction and magnitude of
force ( F), acceleration ( a) and velocity ( v) during the motion. Note that both force and
acceleration act in the downward direction during the motion.
4: When force is applied perpendicular to the direction of motion, then it causes change in the
direction of the velocity.
A simple change of direction also constitutes change in velocity and, therefore, acceleration.
Consider the case of a uniform circular motion in which a particle moves along a circular path at
constant speed “v”. Let v 1 and v 2 be the velocities of the particle at two time instants, then



Figure 2.9. Uniform circular motion
A central force perpendicular to motion causes change in direction.
In the adjoining figure, the vector segments OC and OD represent v 1 and v 2 . Knowing that vector
difference Δv is directed from initial to final position, it is represented by vector CD. Using the
adjoining vector triangle,
The important thing to realize here is that direction of Δ v is along CD, which is directed towards
the origin. This result is in complete agreement of what we know about uniform circular motion
(The topic of uniform circular motion is covered in separate module). We need to apply a force
(causing acceleration to the moving particle) across (i.e. perpendicular) to the motion to change
direction. If the force (hence acceleration) is perpendicular to velocity, then magnitude of velocity
i.e. speed remains same, whereas the direction of motion keeps changing.
Example 2.3. Acceleration
Problem : An object moves along a quadrant AB of a circle of radius 10 m with a constant
speed 5 m/s. Find the average velocity and average acceleration in this interval.
Solution : Here, we can determine time interval form the first statement of the question. The
particle covers a distance of 2πr/4 with a speed v. Hence, time interval,
Magnitude of average velocity is given by the ratio of the magnitude of displacement and time
:


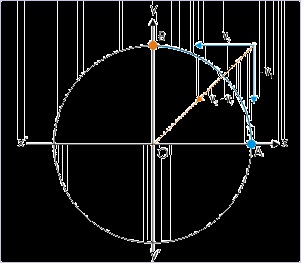


Figure 2.10. Motion along circular path
Average velocity is directed along vector AB i.e. in the direction of displacement vector.
Magnitude of average acceleration is given by the ratio :
Figure 2.11. Motion along circular path
Direction of acceleration
Here,
Average acceleration is directed along the direction of vector v 2 – v 1 i.e. directed towards the
center of the circle (as shown in the figure).



5: When force is applied at a certain angle with the motion, then it causes change in both
magnitude and direction of the velocity. The component of force in the direction of motion
changes its magnitude (an increase or decrease), while the component of force perpendicular to
the direction of motion changes its direction.
The motion of a small spherical mass “m”, tied to a fixed point with the help of a string illustrates
the changes taking place in both the direction and magnitude of the velocity. Saving the details for
discussion at a later point in the course, here tension in the string and tangential force provide for
the change in the direction and magnitude of velocity respectively.
When the string makes at angle, θ, with the vertical, then :
Figure 2.12. Motion of a pendulum
Forces acting on the pendulum bob
(a) Tension in the string, T is :
This force acts normal to the path of motion at all points and causes the body to continuously
change its direction along the circular path. Note that this force acts perpendicular to the direction
of velocity, which is along the tangent at any given point on the arc.
(b) Tangential force, F, is :
This force acts tangentially to the path and is in the direction of velocity of the spherical mass,
which is also along the tangent at that point. As the force and velocity are in the same direction,
this force changes the magnitude of velocity. The magnitude of velocity increases when force acts
in the direction of velocity and magnitude of velocity decreases when force acts in the opposite
direction to that of velocity.
2.3. Acceleration and deceleration*
Acceleration and deceleration are terms which are generally considered to have opposite meaning.
However, there is difference between literal and scientific meanings of these terms. In literal
sense, acceleration is considered to describe an increase or positive change of speed or velocity.
On the other hand, deceleration is considered to describe a decrease or negative change of speed or
velocity. Both these descriptions are incorrect in physics. We need to form accurate and exact
meaning of these two terms. In this module, we shall explore these terms in the context of general
properties of vector and scalar quantities.
A total of six (6) attributes viz time, distance, displacement, speed, velocity and acceleration are
used to describe motion. Three of these namely time, distance and speed are scalar quantities,
whereas the remaining three attributes namely displacement, velocity and acceleration are vectors.
Interpretations of these two groups are different with respect to (ii) negative and positive sign and
(i) sense of increase and decrease. Further these interpretations are also affected by whether we
consider these terms in one or two/three dimensional motion.
The meaning of scalar quantities is more and less clear. The scalar attributes have only magnitude
and no sense of direction. The attributes “distance” and “speed” are positive quantities. There is
no possibility of negative values for these two quantities. In general, time is also positive.
However, it can be assigned negative value to represent a time instant that occurs before the start
of observation. For this reason, it is entirely possible that we may get negative time as solution of
kinematics consideration.
Negative vector quantities
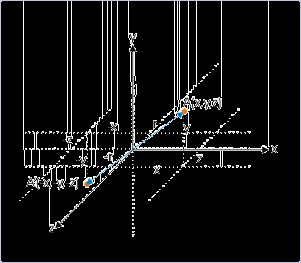
A vector like acceleration may be directed in any direction in three dimensional space, which is
defined by the reference coordinate system. Now, why should we call vector (as shown in the
figure below) represented by line (i) positive and that by line (ii) negative? What is the
qualification for a vector being positive or negative? There is none. Hence, in pure mathematical
sense, a negative vector can not be identified by itself.



Figure 2.13. Vector representation in three dimensional reference
Vectors in isolation have no sense of being negative.
In terms of component vectors, let us represent two accelerations a 1 and a 2 as :
Why should we call one of the above vectors as positive and other as negative acceleration?
Which sign should be considered to identify a positive or negative vector? Further, the negative of
a 1 expressed in component form is another vector given by – a 1 :
So, what is the actual position? The concept of negative vector is essentially a relative concept. If
we represent a vector A as shown in the figure below, then negative to this vector – A is just
another vector, which is directed in the opposite direction to that of vector A and has equal
magnitude as that of A.
In addition, if we denote “- A” as “ B”, then “ A” is “- B”. We, thus, completely loose the
significance of a negative vector when we consider it in isolation. We can call the same vector
either “ A” or “- A”. We conclude, therefore, that a negative vector assumes meaning only in
relation with another vector.
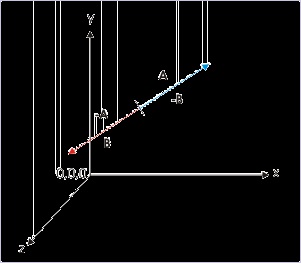
Figure 2.14. Vector representation in three dimensional reference
Vectors in isolation have no sense of being negative.
In one dimensional motion, however, it is possible to assign distinct negative values. In this case,
there are only two directions; one of which is in the direction of reference axis (positive) and the
other is in the opposite direction (negative). The significance of negative vector in one
dimensional motion is limited to relative orientation with respect to reference direction. In the
nutshell, sign of vector quantity in one dimensional motion represents the directional property of
vector. It has only this meaning. We can not attach any other meaning for negating a vector
quantity.
It is important to note that the sequence in “-5 i" is misleading in the sense that a vector quantity
can not have negative magnitude. The negative sign, as a matter of fact, is meant for unit vector “
i”. The correct reading sequence would be “5 x -“ i”, meaning that it has a magnitude of “5” and is
directed in “-“ i” direction i.e. opposite to reference direction. Also, since we are free to choose
our reference, the previously assigned “-5 i” can always be changed to “5 i” and vice-versa.
We summarize the discussion so far as :
There is no independent meaning of a negative vector attribute.
In general, a negative vector attribute is defined with respect to another vector attribute having
equal magnitude, but opposite direction.
In the case of one dimensional motion, the sign represents direction with respect to reference
direction.
“Increase” and “decrease” of vectors quantities
The vector consist of both magnitude and direction. There can be infinite directions of a vector.
On the other hand, increase and decrease are bi-directional and opposite concepts. Can we attach
meaning to a phrase “increase in direction” or “decrease in direction”? There is no sense in saying


that direction of the moving particle has increased or decreased. In the nutshell, we can associate
the concepts of increase and decrease with quantities which are scalar – not quantities which are
vector. Clearly, we can attach the sense of increase or decrease with the magnitudes of velocity or
acceleration, but not with velocity and acceleration.
For this reason, we may recall that velocity is defined as the time rate of “change” – not “increase
or decrease” in displacement. Similarly, acceleration is defined as time rate of change of velocity
– not “increase or decrease” in velocity. It is so because the term “change” conveys the meaning
of “change” in direction as well that of “change” as increase or decrease in the magnitude of a
vector.
However, we see that phrases like “increase or decrease in velocity” or “increase or decrease in
acceleration” are used frequently. We should be aware that these references are correct only in
very specific context of motion. If motion is unidirectional, then the vector quantities associated
with motion is treated as either positive or negative scalar according as it is measured in the
reference direction or opposite to it. Even in this situation, we can not associate concepts of
increase and decrease to vector quantities. For example, how would we interpret two particles
moving in negative x-direction with negative accelerations
and
respectively ?
Which of the two accelerations is greater acceleration ? Algebraically, “-10” is greater than “-20”.
But, we know that second particle is moving with higher rate of change in velocity. The second
particle is accelerating at a higher rate than first particle. Negative sign only indicates that particle
is moving in a direction opposite to a reference direction.
Clearly, the phrases like “increase or decrease in velocity” or “increase or decrease in
acceleration” are correct only when motion is "unidirectional" and in "positive" reference
direction. Only in this restricted context, we can say that acceleration and velocity are increasing
or decreasing. In order to be consistent with algebraic meaning, however, we may prefer to
associate relative measure (increase or decrease) with magnitude of the quantity and not with the
vector quantity itself.
Deceleration
Acceleration is defined strictly as the time rate of change of velocity vector. Deceleration, on the
other hand, is acceleration that causes reduction in "speed". Deceleration is not opposite of
acceleration. It is certainly not negative time rate of change of velocity. It is a very restricted term
as explained below.
We have seen that speed of a particle in motion decreases when component of acceleration is
opposite to the direction of velocity. In this situation, we can say that particle is being decelerated.
Even in this situation, we can not say that deceleration is opposite to acceleration. Here, only a
component of acceleration is opposite to velocity – not the entire acceleration. However, if
acceleration itself (not a component of it) is opposite to velocity, then deceleration is indeed
opposite to acceleration.
If we consider motion in one dimension, then the deceleration occurs when signs of velocity and
acceleration are opposite. A negative velocity and a positive acceleration mean deceleration; a
positive velocity and a negative acceleration mean deceleration; a positive velocity and a positive
acceleration mean acceleration; a negative velocity and a negative acceleration mean acceleration.
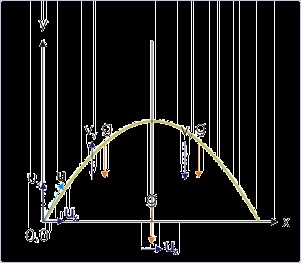
Take the case of projectile motion of a ball. We study this motion as two equivalent linear
motions; one along x-direction and another along y-direction.
Figure 2.15. Parabolic motion
The projected ball undergoes deceleration in y-direction.
For the upward flight, velocity is positive and acceleration is negative. As such the projectile is
decelerated and the speed of the ball in + y direction decreases (deceleration). For downward
flight from the maximum height, velocity and acceleration both are negative. As such the
projectile is accelerated and the speed of the ball in - y direction increases (acceleration).
In the nutshell, we summarize the discussion as :
Deceleration results in decrease in speed i.e magnitude of velocity.
In one dimensional motion, the “deceleration” is defined as the acceleration which is opposite
to the velocity.
Example 2.4. Acceleration and deceleration
Problem : The velocity of a particle along a straight line is plotted with respect to time as
shown in the figure. Find acceleration of the particle between OA and CD. What is
acceleration at t = 0.5 second and 1.5 second. What is the nature of accelerations in different
segments of motion? Also investigate acceleration at A.
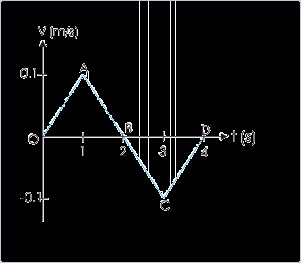




Figure 2.16. Velocity – time plot
Solution : Average acceleration between O and A is given by the slope of straight line OA :
Average acceleration between C and D is given by the slope of straight line CD :
Accelerations at t = 0.5 second and 1.5 second are obtained by determining slopes of the curve
at these time instants. In the example, the slopes at these times are equal to the slope of the
lines OA and AB.
Instantaneous acceleration at t = 0.5 s :
Instantaneous acceleration at t = 1.5 s :
We check the direction of velocity and acceleration in different segments of the motion in
order to determine deceleration. To enable comparision, we determine directions with respect
to the assumed positive direction of velocity. In OA segment, both acceleration and velocity
are positive (hence particle is accelerated). In AB segment, acceleration is negative, but
velocity is positive (hence particle is decelerated). In BC segment, both acceleration and
velocity are negative (hence particle is accelerated). In CD segment, acceleration is positive
but velocity is negative (hence particle is decelerated).
Alternatively, the speed increases in segment OA and BC (hence acceleration); decreases in
segments AB and CD (hence deceleration).
We note that it is not possible to draw an unique tangent at point A. We may draw infinite
numbers of tangent at this point. In other words, limit of average acceleration can not be
evaluated at A. Acceleration at A, therefore, is indeterminate.
Graphical interpretation of negative vector quantities describing
motion
Position vector
We may recall that position vector is drawn from the origin of reference to the position occupied
by the body on a scale taken for drawing coordinate axes. This implies that the position vector is
rooted to the origin of reference system and the position of the particle. Thus, we find that
position vector is tied at both ends of its graphical representation.
Also if position vector ‘ r’ denotes a particular position (A), then “- r” denotes another position
(A’), which is lying on the opposite side of the reference point (origin).
Figure 2.17. Position vector
Velocity vector
The velocity vector, on the other hand, is drawn on a scale from a particular position of the object
with its tail and takes the direction of the tangent to the position curve at that point. Also, if
velocity vector ‘ v’ denotes the velocity of a particle at a particular position, then “- v” denotes
another velocity vector, which is reversed in direction with respect to the velocity vector, v.
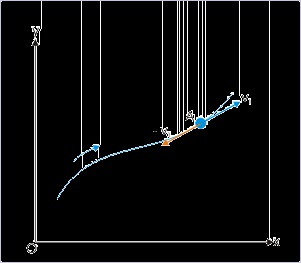
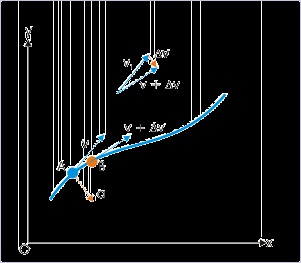
Figure 2.18. Velocity vector
In either case (positive or negative), the velocity vectors originate from the position of the particle
and are drawn along the tangent to the motion curve at that point. It must be noted that veloci




































