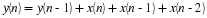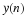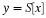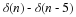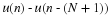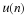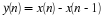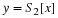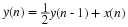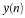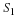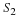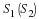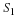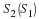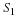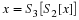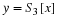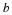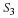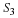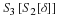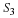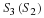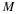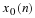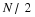Deriving the DFT from the DTFT
Truncating the Time-domain Signal
The DTFT usually cannot be computed exactly because
the sum in Equation 8.1 is infinite.
However, the DTFT may be approximately computed
by truncating the sum to a finite window.
Let w(n) be a rectangular window of length N:
Then we may define a truncated signal to be
The DTFT of x tr (n) is given by:
We would like to compute 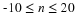 , but as with
filter design, the truncation window distorts
the desired frequency characteristics;
, but as with
filter design, the truncation window distorts
the desired frequency characteristics;
 and
and 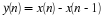 are generally not equal.
To understand the relation between these two DTFT's,
we need to convolve in the frequency domain (as we did
in designing filters with the truncation
technique):
are generally not equal.
To understand the relation between these two DTFT's,
we need to convolve in the frequency domain (as we did
in designing filters with the truncation
technique):
where 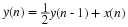 is the DTFT of w(n).
Equation 8.8 is the periodic convolution of
is the DTFT of w(n).
Equation 8.8 is the periodic convolution of 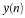 and
and 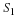 .
Hence the true DTFT,
.
Hence the true DTFT, 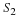 ,
is smoothed via convolution with
,
is smoothed via convolution with 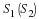 to produce the truncated DTFT,
to produce the truncated DTFT, 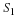 .
.
We can calculate  :
:
For ω≠0,±2π,..., we have:
Notice that the magnitude of this function
is similar to sinc(ωN/2)
except that it is periodic in ω with period 2π.
Equation 8.7 contains a summation over a finite number of terms.
However, we can only evaluate
Equation 8.7 for a finite set of frequencies, ω.
We must sample in the frequency domain to compute the DTFT on a computer.
We can pick any set of frequency points
at which to evaluate Equation 8.7,
but it is particularly useful to uniformly sample ω at N points,
in the range [0,2π).
If we substitute
(8.11)
ω
=
2
π
k
/
N
for k=0,1,...(N–1) in
Equation 8.7,
we find that
In short, the DFT values result from sampling the DTFT
of the truncated signal.
Download
DTFT.m for the following section.
We will next investigate the effect of windowing when computing
the DFT of the signal 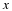 truncated with a window of size N=20.
truncated with a window of size N=20.
In the same figure, plot the phase and magnitude
of 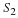 , using equations Equation 8.9 and
Equation 8.10.
, using equations Equation 8.9 and
Equation 8.10.
Determine an expression for 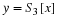 (the DTFT of the non-truncated signal).
(the DTFT of the non-truncated signal).
Truncate the signal x(n) using a window of size N=20
and then use
DTFT.m
to compute 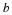 .
Make sure that the plot contains a least 512 points.
.
Make sure that the plot contains a least 512 points.
Hint
Use the command [X,w] = DTFT(x,512)
.
Plot the magnitude of 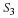 .
.
INLAB REPORT
Submit the plot of the phase and magnitude of 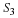 .
.
Submit the analytical expression for 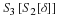 .
.
Submit the magnitude plot of 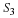 .
.
Describe the difference between  and
and 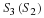 . What is the reason for this difference?
. What is the reason for this difference?
Comment on the effects of using a different window for w(n).
For example, what would you expect your plots to look like if you
had used
a Hamming window in place of the truncation (rectangular) window?
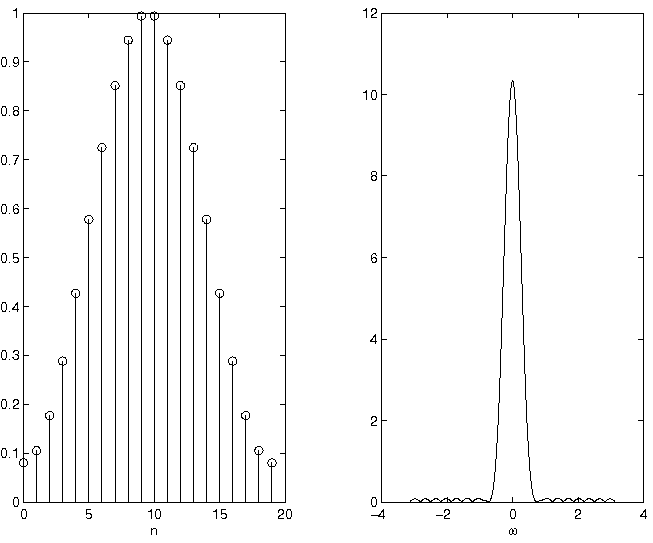
(See Figure 8.1 for a plot of a Hamming window of length
20 and its DTFT.)