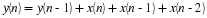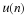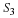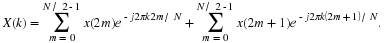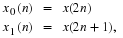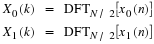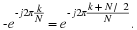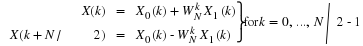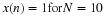Continuation of DFT Analysis
This section continues the analysis of the DFT started in the
previous week's laboratory.
Shifting the Frequency Range
In this section, we will illustrate a representation for the DFT of
Equation 9.1 that is a bit more intuitive. First create a Hamming window
x of length N=20, using the Matlab command
x = hamming(20)
.
Then use your Matlab function DFTsum to compute the 20 point
DFT of x.
Plot the magnitude of the DFT, |X20(k)|, versus the index k.
Remember that the DFT index k starts at 0 not 1!
INLAB REPORT
Hand in the plot of the |X20(k)|.
Circle the regions of the plot corresponding to low frequency components.
Our plot of the DFT has two disadvantages.
First, the DFT values are plotted against k rather then
the frequency ω.
Second, the arrangement of frequency samples in the DFT
goes from 0 to 2π rather than from –π to π,
as is conventional with the DTFT.
In order to plot the DFT values similar to a conventional DTFT plot,
we must compute the vector of frequencies in radians per sample,
and then “rotate” the plot to produce the more familiar
range, –π to π.
Let's first consider the vector w
of frequencies in radians per sample.
Each element of w
should be the frequency of the
corresponding DFT sample X(k), which can be computed by
However, the frequencies
should also lie in the range from –π to π.
Therefore, if ω≥π, then it should be
set to ω–2π. An easy way of making this change in
Matlab 5.1 is
w(w>=pi) = w(w>=pi)-2*pi
.
The resulting vectors X
and w
are correct,
but out of order. To reorder them,
we must swap the first and second halves of the
vectors. Fortunately, Matlab provides a function specifically for
this purpose, called fftshift.
Write a Matlab function to compute samples of the DTFT
and their corresponding frequencies in the range –π to π.
Use the syntax
[X,w] = DTFTsamples(x)
where x
is an N point vector, X
is the length N vector
of DTFT samples, and w
is the length N vector of corresponding
radial frequencies.
Your function DTFTsamples should call your function
DFTsum and use the Matlab function fftshift.
Use your function DTFTsamples to compute
DTFT samples of the Hamming window of length N=20.
Plot the magnitude of these DTFT samples versus frequency
in rad/sample.
INLAB REPORT
Hand in the code for your function DTFTsamples.
Also hand in the plot of the magnitude of the DTFT samples.
The spacing between samples of the DTFT is determined
by the number of points in the DFT.
This can lead to surprising results when the number
of samples is too small.
In order to illustrate this effect,
consider the finite-duration signal
In the following, you will compute the DTFT samples of x(n)
using both N=50 and N=200 point DFT's.
Notice that when N=200, most of the samples of x(n) will be
zeros because x(n)=0 for n≥50.
This technique is known as “zero padding”, and may be used to
produce a finer sampling of the DTFT.
For N=50 and N=200, do the following:
Compute the vector x
containing the values x(0),⋯,x(N–1).
Compute the samples of X(k) using your function
DTFTsamples.
Plot the magnitude of the DTFT samples versus frequency
in rad/sample.
INLAB REPORT
Submit your two plots of the DTFT samples for N=50 and N=200.
Which plot looks more like the true DTFT?
Explain why the plots look so different.
The Fast Fourier Transform Algorithm
We have seen in the preceding sections that the DFT
is a very computationally intensive
operation. In 1965, Cooley and Tukey (1)
published an algorithm that could
be used to compute the DFT much more efficiently.
Various forms of their algorithm,
which came to be known as the fast Fourier transform (FFT), had actually
been developed much earlier by other mathematicians (even dating back to
Gauss). It was their paper, however, which stimulated a revolution in the field
of signal processing.
It is important to keep in mind at the outset that the FFT is not
a new transform.
It is simply a very efficient way to compute an existing
transform, namely the DFT.
As we saw, a straight forward implementation of the DFT can
be computationally expensive because the number of multiplies
grows as the square of the input length (i.e. N2 for an N point DFT).
The FFT reduces this computation using two simple but important
concepts.
The first concept, known as divide-and-conquer,
splits the problem into two smaller problems.
The second concept, known as recursion, applies this divide-and-conquer
method repeatedly until the problem is solved.
Consider the defining equation for the DFT and assume that N is even,
so that N/2 is an integer:
Here we have dropped the subscript of N in the notation
for X(k).
We will also use the notation
(9.5)
X
(
k
)
=
DFTN
[x ( n )]
to denote the N point DFT of the signal x(n).
Suppose we break the sum in Equation 9.4 into two sums, one containing
all the terms for which n is even, and one containing all the terms for
which n is odd:
We can eliminate the conditions “n even” and “n odd” in
Equation 9.6 by making a
change of variable in each sum. In the first sum, we replace n by 2m.
Then as we sum m from 0 to N/2–1, n=2m will take on all even
integer values between 0 and N–2. Similarly, in the second sum, we
replace n by 2m+1. Then as we sum m from 0 to N/2–1,
n=2m+1 will take on all odd
integer values between 0 and N–1.
Thus, we can write
Next we rearrange the exponent of the complex exponential in the first
sum, and split and rearrange the exponent in the second sum to yield
Now compare the first sum in Equation 9.8 with the definition
for the DFT given by Equation 9.4. They have exactly the same form if
we replace N everywhere in Equation 9.4 by N/2. Thus the first sum
in Equation 9.8 is an N/2 point DFT of the even-numbered
data points in the original sequence. Similarly, the second sum
in Equation 9.8 is an N/2 point DFT of the odd-numbered
data points in the original sequence. To obtain the N point DFT of the
complete sequence, we multiply the DFT of the odd-numbered data points
by the complex exponential factor e–j2πk/N, and then simply
sum the two N/2 point DFTs.
To summarize, we will rewrite Equation 9.8 according to this
interpretation.
First, we define two new N/2 point data sequences x0(n) and
x1(n), which contain the even and odd-numbered data
points from the original N point sequence, respectively:
where n=0,...,N/2–1.
This separation of even and odd points is called decimation in time.
The N point DFT of x(n) is then given by
where X0(k) and X1(k) are the N/2 point DFT's of the even and odd points.
While Equation 9.10 requires less computation
than the original N point DFT,
it can still be further simplified.
First, note that each N/2 point DFT is periodic
with period N/2.
This means that we need to only compute X0(k) and X1(k)
for N/2 values of k rather than the N values
shown in Equation 9.10.
Furthermore, the complex exponential factor e–j2πk/N
has the property that
These two facts may be combined to yield a simpler
expression for the N point DFT:
where the complex constants defined by WNk=e–j2πk/N
are commonly known as the twiddle factors.
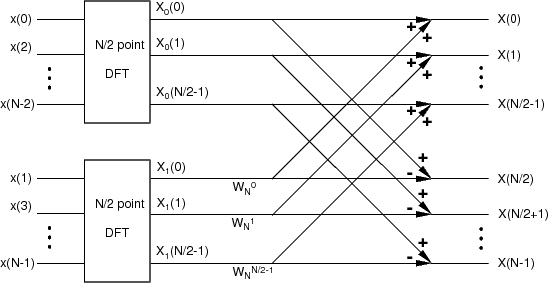
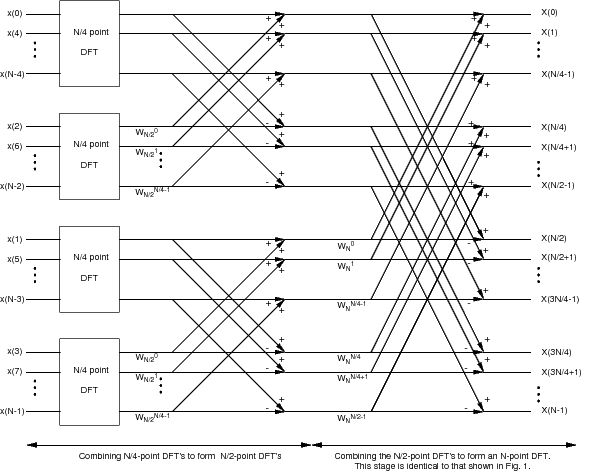
Figure 9.1
shows a graphical interpretation of Equation 9.13
which we will refer to as the “divide-and-conquer DFT”.
We start on the left side with the data separated into
even and odd subsets.
We perform an N/2 point DFT on each subset,
and then multiply the output of the odd DFT by the required twiddle
factors.
The first half of the output is computed by adding
the two branches,
while the second half is formed by subtraction.
This type of flow diagram is conventionally used to describe a
fast Fourier transform algorithm.
Implementation of Divide-and-Conquer DFT
In this section, you will implement the DFT transformation
using Equation 9.13 and the illustration
in Figure 9.1.
Write a Matlab function with the syntax
X = dcDFT(x)
where x
is a vector of even length N,
and X
is its DFT.
Your function dcDFT should do the following:
Separate the samples of x
into even and odd points.
Hint
The Matlab command
x0 = x(1:2:N)
can be used to obtain the “even” points.
Use your function DFTsum to compute the two
N/2 point DFT's.
Multiply by the twiddle factors WNk=e–j2πk/N.
Combine the two DFT's to form X.
Test your function dcDFT by using it to compute the DFT's
of the following signals.
x(n)=δ(n) for N=10
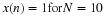
x(n)=ej2πn/N for N=10
INLAB REPORT
Submit the code for your function dcDFT.
Determine the number of multiplies that are required in this approach
to computing an N point DFT.
(Consider a multiply to be one multiplication of
real or complex numbers.)
HINT
Refer to the diagram of Figure 9.1, and remember
to consider the N/2 point DFTs.
Recursive Divide and Conquer
The second basic concept underlying the FFT algorithm is that of recursion.
Suppose N/2 is also even.
Then we may apply the same decimation-in-time
idea to the computation of each of the N/2 point DFT's
in