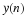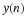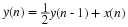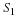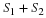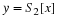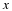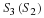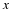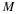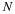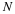This is the second part of a two week experiment. During the
first week
we discussed basic properties
of speech signals, and performed some simple analyses in the time and frequency
domain.
This week, we will introduce a system model for speech production.
We will cover some background on linear predictive coding,
and the final exercise will bring all the prior material together in a
speech coding exercise.
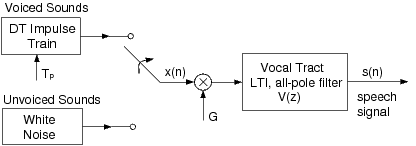
From a signal processing standpoint, it is very useful to think of speech
production in terms of a model, as in Figure 15.1.
The model shown is the simplest of its kind,
but it includes all the principal components.
The excitations for voiced and unvoiced speech are represented by an
impulse train and white noise generator, respectively.
The pitch of voiced speech is controlled by the spacing between
impulses, Tp, and
the amplitude (volume) of the excitation is controlled by the gain factor G.
As the acoustical excitation travels from its source (vocal cords,
or a constriction), the shape of the vocal tract alters the spectral
content of the signal.
The most prominent effect is the formation of resonances, which
intensifies the signal energy at certain frequencies (called formants).
As we learned in the Digital Filter Design lab, the amplification of certain
frequencies may be achieved with a linear filter by an appropriate
placement of poles in the transfer function.
This is why the filter in our speech model utilizes an all-pole LTI filter.
A more accurate model might include a few zeros in the transfer function,
but if the order of the filter is chosen appropriately, the all-pole model
is sufficient.
The primary reason for using the all-pole model is the distinct computational
advantage in calculating the filter coefficients, as will be discussed
shortly.
Recall that the transfer function of an all-pole filter has the form
where P is the order of the filter.
This is an IIR filter that may
be implemented with a recursive difference equation.
With the input G·x(n), the speech signal s(n) may be written as
Keep in mind that the filter coefficients will change continuously as
the shape of the vocal tract changes, but speech segments of an
appropriately small length may be approximated by a time-invariant model.
This speech model is used in a variety of speech processing applications,
including methods of speech recognition, speech coding for transmission,
and speech synthesis.
Each of these applications of the model involves dividing the speech signal
into short segments, over which the filter coefficients are almost constant.
For example, in speech transmission the bit rate can be significantly
reduced by dividing the signal up into segments, computing and sending
the model parameters for each segment (filter coefficients, gain, etc.),
and re-synthesizing the signal at the receiving end, using a model
similar to Figure 15.1.
Most telephone systems use some form of this approach.
Another example is speech recognition.
Most recognition methods involve comparisons between short
segments of the speech signals, and the filter coefficients of this model
are often used in computing the “difference" between segments.
Synthesis of Voiced Speech
Download the file
coeff.mat for the following section.
Download the file
coeff.mat
and load it into the
Matlab workspace using the load command.
This will load three sets of filter coefficients: A1, A2, and A3
for the vocal tract model in
Equation 15.1 and Equation 15.2.
Each vector contains coefficients 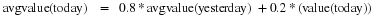 for an all-pole filter of order 15.
for an all-pole filter of order 15.
We will now synthesize voiced speech segments for each of these sets of
coefficients.
First write a Matlab function x=exciteV(N,Np)
which creates a
length N excitation for voiced speech, with a pitch period of Np
samples.
The output vector x should contain a discrete-time impulse train
with period Np (e.g. [1 0 0 ⋯ 0 1 0 0 ⋯]).
Assuming a sampling frequency of 8 kHz (0.125 ms/sample),
create a 40 millisecond-long excitation with a pitch period of 8 ms,
and filter it using Equation 15.2 for each set of coefficients.
For this, you may use the command
s = filter(1,[1 -A],x)
where A is the row vector of filter coefficients
(see Matlab's help on filter for details).
Plot each of the three filtered signals.
Use subplot()
and orient tall
to place them in the same figure.
We will now compute the frequency response of each of these filters.
The frequency response may be obtained by evaluating
Equation 15.1 at points along z=ejω.
Matlab will compute this with the command [H,W]=freqz(1,[1 -A],512)
,
where A is the vector of coefficients.
Plot the magnitude of each response versus frequency in Hertz.
Use subplot()
and orient tall
to plot them in
the same figure.
The location of the peaks in the spectrum correspond
to the formant frequencies.
For each vowel signal, estimate the first three formants (in Hz) and list them
in the figure.
Now generate the three signals again, but use an excitation which is 1-2
seconds long.
Listen to the filtered signals using soundsc.
Can you hear qualitative differences in the signals?
Can you identify the vowel sounds?
INLAB REPORT
Hand in the following:
A figure containing the three time-domain plots of the voiced signals.
Plots of the frequency responses for the three filters.
Make sure to label the frequency axis in units of Hertz.
For each of the three filters, list the approximate center
frequency of the first three formant peaks.
Comment on the audio quality of the synthesized signals.
The filter coefficients which were provided in the previous section were
determined using a technique called linear predictive coding (LPC).
LPC is a fundamental component of many speech processing applications,
including compression, recognition, and synthesis.
In the following discussion of LPC, we will view the speech signal as a
discrete-time random process.
Forward Linear Prediction
Suppose we have a discrete-time random process
 whose elements have some degree of
correlation.
The goal of forward linear prediction is to predict the sample Sn
using a linear combination of the previous P samples.
whose elements have some degree of
correlation.
The goal of forward linear prediction is to predict the sample Sn
using a linear combination of the previous P samples.
P is called the order of the predictor.
We may represent the error of predicting Sn by a random sequence en.
An optimal set of prediction coefficients ak for Equation 15.4
may be determined by minimizing the mean-square error 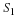 .
Note that since the error is generally a function of n,
the prediction coefficients will also be functions of n.
To simplify notation, let us first define the following column vectors.
.
Note that since the error is generally a function of n,
the prediction coefficients will also be functions of n.
To simplify notation, let us first define the following column vectors.
Then,
The second and third terms of Equation 15.7 may be written
in terms of the autocorrelation sequence rSS(k,l).
Substituting into Equation 15.7, the mean-square
error may be written as
(15.10)
E
[en2]
=
E
[Sn2]
–
2
aTrS
+
aTRSa
Note that while a
and rS are vectors, and RS
is a matrix,
the expression in Equation 15.10 is still a scalar quantity.
To find the optimal ak coefficients, which we will call  ,
we differentiate Equation 15.10 with respect to the
vector a (compute the gradient),
and set it equal to the zero vector.
,
we differentiate Equation 15.10 with respect to the
vector a (compute the gradient),
and set it equal to the zero vector.
Solving,
The vector equation in Equation 15.12 is a system of P scalar
linear equations, which may be solved by inverting the matrix RS.
Note from Equation 15.8 and Equation 15.9 that rS and
RS are generally functions of n.
However, if Sn is wide-sense stationary, the autocorrelation function
is only dependent
on the difference between the two indices, rSS(k,l)=rSS(|k–l|).
Then RS and rS are no longer dependent on n,
and may be written as follows.
Therefore, if Sn is wide-sense stationary, the optimal ak coefficients
do not depend on n.
In this case, it is also important to note that
RS is a Toeplitz (constant along diagonals) and
symmetric matrix, which allows Equation 15.12 to be solved efficiently
using the Levinson-Durbin algorithm (see 1).
This property is essential for many real-time applications of linear
prediction.
Linear Predictive Coding of Speech
An important question has yet to be addressed.
The solution in Equation 15.12 to the linear prediction problem
depends entirely on the autocorrelation sequence.
How do we estimate the autocorrelation of a speech signal?
Recall that the applications to which we are applying LPC
involve dividing the speech signal up into short segments and computing
the filter coefficients for each segment.
Therefore we need to consider the problem of estimating the autocorrelation
for a short segment of the signal.
In LPC, the following "biased" autocorrelation estimate is
often used.
Here we are assuming we have a length N segment which starts at n=0.
Note that this is the single-parameter form of the autocorrelation
sequence, so that the forms in
Equation 15.13 and Equation 15.14 may be used for
rS and RS.
Download the file
test.mat for this exercise.
Write a function coef=mylpc(x,P)
which will compute the order-P
LPC coefficients for the column vector x, using the autocorrelation method
(“lpc" is a built-in Matlab function, so use the name mylpc).
Consider the input vector x as a speech segment, in other words
do not divide it up into pieces.
The output vector coef should be a column vector containing the
P coefficients
 .
In your function you should do the following:
.
In your function you should do the following:
Compute the biased autocorrelation estimate of Equation 15.15
for the lag values 0≤m≤P.
You may use the xcorr function for this.
Form the rS and RS vectors as in
Equation 15.13 and Equation 15.14.
Hint: Use the toeplitz function to form RS.
Solve the matrix equation in Equation 15.12 for
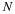 .
.
To test your function, download the file
test.mat,
and load it into Matlab.
This file contains two vectors: a signal x and its order-15 LPC
coefficients a.
Use your function to compute the order-15 LPC coefficients of x, and
compare the result to the vector a.
INLAB REPORT
Hand in your mylpc function.
Speech Coding and Synthesis
Download the file
phrase.au for the following section.
One very effective application of LPC is the compression
of speech signals.
For example, an LPC vocoder (voice-coder) is a system used in
many telephone systems to reduce the bit rate for the transmission of speech.
This system has two overall components:
an analysis section which computes signal
parameters (gain, filter coefficients, etc.), and a synthesis section which
reconstructs the speech signal after transmission.
Since we have introduced the speech model in "A Speech Model",
and the estimation of LPC coefficients in "Linear Predictive Coding",
we now have all the tools necessary to implement a simple vocoder.
First, in the analysis section,
the original speech signal will be split into short time frames.
For each frame, we will compute the signal energy, the LPC coefficients,
and determine whether the segment is voiced or unvoiced.
Download the file
phrase.au.
This speech signal is sampled at a rate of 8000 Hz.
Divide the original speech signal into 30ms non-overlapping frames.
Place the frames into L consecutive columns of a matrix S
(use reshape).
If the samples at the tail end of the signal do not fill an entire
column, you may disregard these samples.
Compute the energy of each frame of the original word, and place
these values in a length L vector called energy.
Determine whether each frame is voiced or unvoiced.
Use your zero_cross function from
the first week
to compute
the number of zero-crossings in each frame.
For length N segments with less than 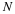 zero-crossings,
classify the segment as voiced, otherwise unvoiced.
Save the results in a vector VU which takes the value of “1" for
voiced and “0" for unvoiced.
zero-crossings,
classify the segment as voiced, otherwise unvoiced.
Save the results in a vector VU which takes the value of “1" for
voiced and “0" for unvoiced.
Use your mylpc functio