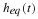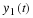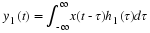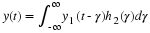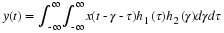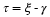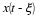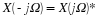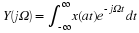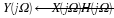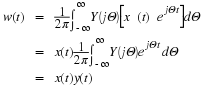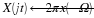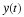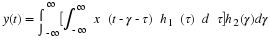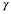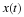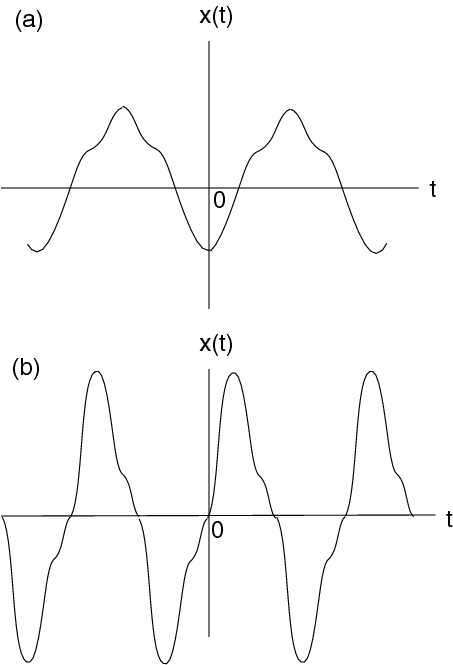
A signal has even symmetry of it satisfies:
and odd symmetry if it satisfies
Figure 2.1 shows pictures of periodic even and odd symmetric signals. If x(t) is an odd symmetric periodic signal, then we must have:
This is easy to see if we choose t0=–T/2.
We also note that the product of two even signals is also even while the product of an even signal and an odd signal must be odd. Finally, the product of two odd signals must be even. For example, suppose xo(t) has odd symmetry and xe(t) has even symmetry. Their product has odd symmetry because if y(t)=xo(t)xe(t), then y(–t)=xo(–t)xe(–t)=–y(t).
A major goal of this book is to develop tools which will enable us to study the frequency content of signals. An important first step is the Fourier Series. The Fourier Series enables us to completely characterize the frequency content of a periodic signal[2]. A periodic signal x(t) can be expressed in terms of the Fourier Series, which is given by:
where
is the fundamental frequency of the periodic signal. Examination of Equation 2.4 suggests that periodic signals can be represented as a sum of suitably scaled cosine and sine waveforms at frequencies of Ω0,2Ω0,3Ω0,.... The cosine and sine terms at frequency nΩ0 are called the nth harmonics. Evidently, periodic signals contain only the fundamental frequency and its harmonics. A periodic signal cannot contain a frequency that is not an integer multiple of its fundamental frequency.
In order to find the Fourier Series, we must compute the Fourier Series coefficients. These are given by
From our discussion of even and odd symmetric signals, it is clear that if x(t) is even, then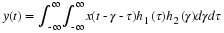 
must be odd and so bn=0. Also if, x(t) has odd symmetry, then 
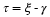also has odd symmetry and hence an=0 (see exercise ???). Moreover, if a signal is even, since 
is also even, if we use the fact that for any even symmetric periodic signal v(t),
then setting t0=–T/2 in Equation 2.7 gives,
This can sometimes lead to a savings in the number of integrals that must be computed. Similarly, if x(t) has odd symmetry, we have
Example 2.1 Consider the signal in Figure 2.2. This signal has even symmetry, hence all of the bn=0. We compute a0 using,
which we recognize as the area of one period, divided by the period. Hence, a0=τ/T. Next, using Equation 2.7 we get
Note how the limits of integration only go from –τ/2 to τ/2 since x(t) is zero everywhere else. Evaluating this integral leads to
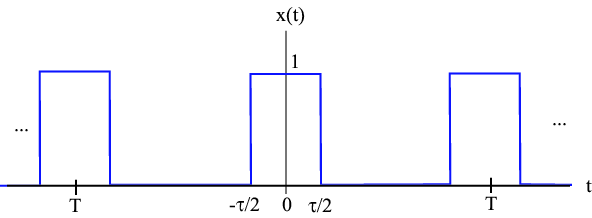
Figure 2.3 shows the first few Fourier Series coefficients for τ=1/2 and T=1. If we attempt to reconstruct x(t) based on only a limited number (say, N) of Fourier Series coefficients, we have
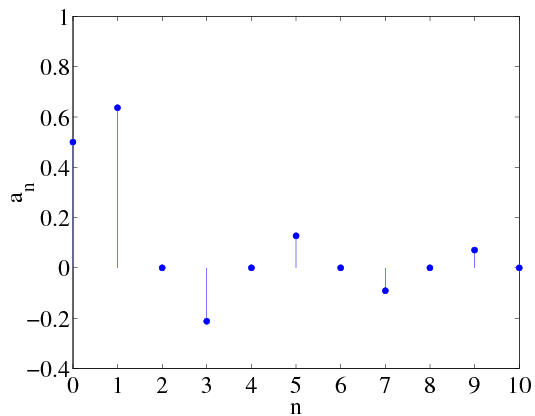
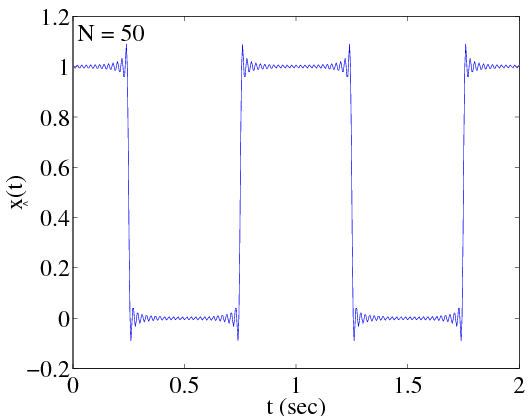
Figures Figure 2.4 and Figure 2.5 show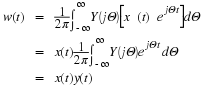 
for N=10, and N=50, respectively.
The ringing characteristic is known as Gibb's phenomenon and disappears only as N approaches ∞.
The following example looks at the Fourier series of an odd-symmetric signal, a sawtooth signal.
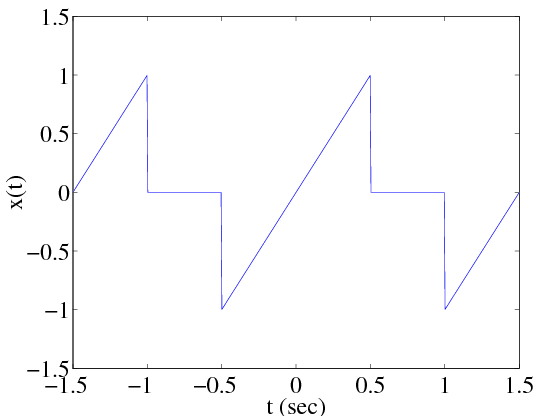
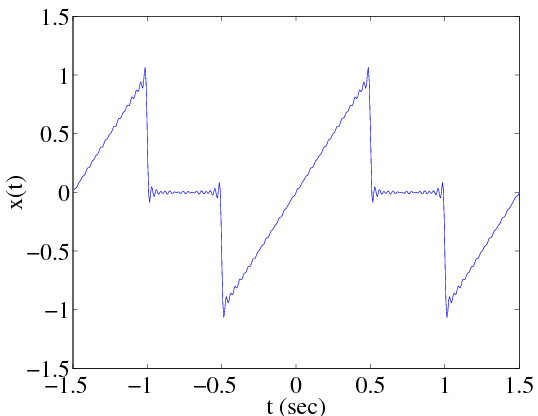
Example 2.2 Now let's compute the Fourier series for the signal in Figure 2.6. The signal is odd-symmetric, so all of the an are zero. The period is T=3/2, hence Ω0=4π/3. Using Equation 2.8, the bn coefficients are found by computing the following integral,
After integrating by parts, we get
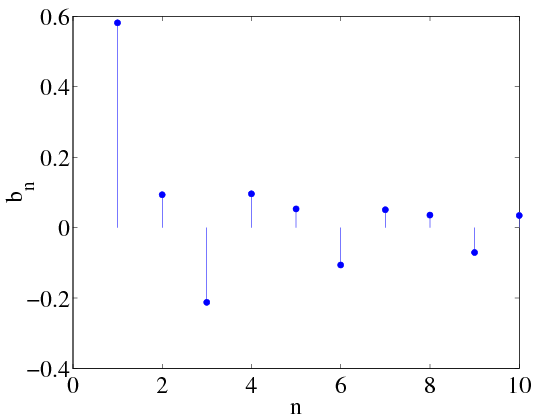
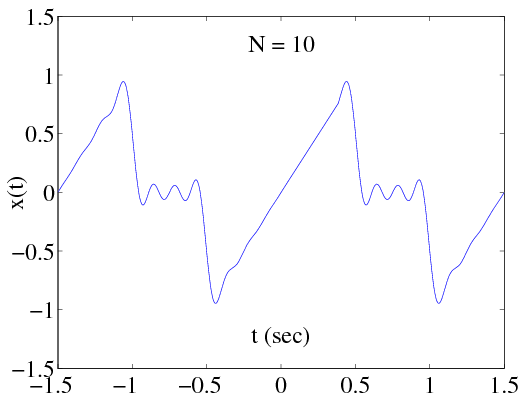
These are plotted in Figure 2.7 and approximations of x(t) using N=10 and N=50 coefficients are shown in Figures Figure 2.8 and Figure 2.9, respectively.
Periodic signals having half-wave symmetry have the property
It turns out that signals with this type of symmetry only have odd-numbered harmonics, the even harmonics are zero. To see this, lets look at the formula for the coefficients an:
Making the substitution τ=t–T/2 in I2 gives
The quantity 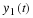can be simplified using the trigonometric identity
We have
Therefore
and we can write:
From this expression we find that an=0 whenever n is even. In fact, we have
A similar derivation leads to
A good choice of t0 can lead to a considerable savings in time when calculating the Fourier Series of half-wave symmetric signals.
Note that half-wave symmetric signals need not have odd or even symmetry for the above formulae to apply. If a signal has half-wave symmetry and in addition has odd or even symmetry, then some additional simplification is possible. Consider the case when a half-wave symmetric signal also has even symmetry. Then clearly bn=0, and Equation 2.25 applies. However since the integrand in Equation 2.25 is the product of two even signals, x(t) and 
, it too has even symmetry. Therefore, instead of integrating from, say, –T/4 to T/4, we need only integrate from 0 to T/4 and multiply the result by 2. Therefore the formula for an for an even, half-wave symmetric signal becomes:
For an odd half-wave symmetric signals, a similar argument leads to
Consider the trigonometric form of the Fourier series
It is important to state under what conditions this series (the right-hand side of Equation 2.31) will actually converge to
