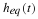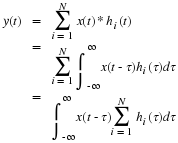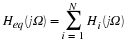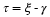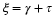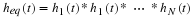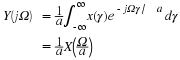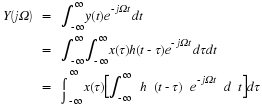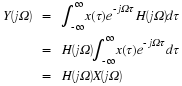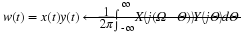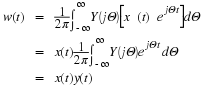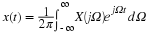Signals, Systems, and Society by Carlos E. Davila - HTML preview

/ Home / Teacher's Resources / Signals, Systems, and Society
PLEASE NOTE: This is an HTML preview only and some elements such as links or page numbers may be incorrect.
Download the book in PDF, ePub, Kindle for a complete version.
PREV   NEXT

Chapter 3. The Fourier Transform

3.1. Derivation of the Fourier Transform*

Let's begin by writing down the formula for the complex form of the Fourier Series:

(3.1)
_autogen-svg2png-0001.png

as well as the corresponding Fourier Series coefficients:

(3.2)
_autogen-svg2png-0002.png

As was mentioned in Chapter 2, as the period T gets large, the Fourier Series coefficients represent more closely spaced frequencies. Lets take the limit as the period T goes to infinity. We first note that the fundamental frequency approaches a differential

(3.3)
_autogen-svg2png-0005.png

consequently

(3.4)
_autogen-svg2png-0006.png

The nth harmonic, nΩ0, in the limit approaches the frequency variable Ω

(3.5) n Ω0 → Ω

From equation Equation 3.2, we have

(3.6) cnT → ∫∞ – ∞ x ( t ) e – j Ω t d t

The right hand side of Equation 3.6 is called the Fourier Transform of x(t):

(3.7) X ( j Ω ) ≡ ∫∞ – ∞ x ( t ) e – j Ω t d t

Now, using Equation 3.6, Equation 3.4, and Equation 3.5 in equation Equation 3.1 gives

(3.8)
_autogen-svg2png-0014.png

which corresponds to the inverse Fourier Transform. Equations Equation 3.7 and Equation 3.8 represent what is known as a transform pair. The following notation is used to denote a Fourier Transform pair

(3.9) x ( t ) ↔ X ( j Ω )

We say that x(t) is a time domain signal while X(jΩ) is a frequency domain signal. Some additional notation which is sometimes used is

(3.10) X ( j Ω ) = F {x ( t )}

and

(3.11) x ( t ) = F – 1 {X ( j Ω )}

References

3.2. Properties of the Fourier Transform*

Properties of the Fourier Transform

The Fourier Transform (FT) has several important properties which will be useful:

  1. Linearity:

    (3.12)αx1(t)+βx2(t)↔αX1(jΩ)+βX2(jΩ)

    where α and β are constants. This property is easy to verify by plugging the left side of Equation 3.12 into the definition of the FT.

  2. Time shift:

    (3.13)x(t–τ)↔e–jΩτX(jΩ)

    To derive this property we simply take the FT of x(t–τ)

    (3.14)∫∞–∞x(t–τ)e–jΩtdt

    using the variable substitution γ=t–τ leads to

    (3.15)t=γ+τ

    and

    (3.16)dγ=dt

    We also note that if t=±∞ then τ=±∞. Substituting Equation 3.15, Equation 3.16, and the limits of integration into Equation 3.14 gives

    (3.17)
    _autogen-svg2png-0012.png

    which is the desired result.

  3. Frequency shift:

    (3.18)
    _autogen-svg2png-0013.png

    Deriving the frequency shift property is a bit easier than the time shift property. Again, using the definition of FT we get:

    (3.19)
    _autogen-svg2png-0014.png

  4. Time reversal:

    (3.20)x(–t)↔X(–jΩ)

    To derive this property, we again begin with the definition of FT:

    (3.21)∫∞–∞x(–t)e–jΩtdt

    and make the substitution γ=–t. We observe that dt=–dγ and that if the limits of integration for t are ±∞, then the limits of integration for γ are ∓γ. Making these substitutions into Equation 3.21 gives

    (3.22)
    _autogen-svg2png-0023.png

    Note that if x(t) is real, then X(–jΩ)=X(jΩ)*.

  5. Time scaling: Suppose we have y(t)=x(at),a>0. We have

    (3.23)Y(jΩ)=∫∞–∞x(at)e–jΩtdt

    Using the substitution γ=at leads to

    (3.24)
    _autogen-svg2png-0029.png

  6. Convolution: The convolution integral is given by

    (3.25)y(t)=∫∞–∞x(τ)h(t–τ)dτ

    The convolution property is given by

    (3.26)Y(jΩ)↔X(jΩ)H(jΩ)

    To derive this important property, we again use the FT definition:

    (3.27)
    _autogen-svg2png-0032.png

    Using the time shift property, the quantity in the brackets is e–jΩτH(jΩ), giving

    (3.28)
    _autogen-svg2png-0034.png

    Therefore, convolution in the time domain corresponds to multiplication in the frequency domain.

  7. Multiplication (Modulation):

    (3.29)
    _autogen-svg2png-0035.png

    Notice that multiplication in the time domain corresponds to convolution in the frequency domain. This property can be understood by applying the inverse Fourier Transform ??? to the right side of Equation 3.29

    (3.30)
    _autogen-svg2png-0036.png

    The quantity inside the brackets is the inverse Fourier Transform of a frequency shifted Fourier Transform,

    (3.31)
    _autogen-svg2png-0037.png

  8. Duality: The duality property allows us to find the Fourier transform of time-domain signals whose functional forms correspond to known Fourier transforms, X(jt). To derive the property, we start with the inverse Fourier transform:

    (3.32)
    _autogen-svg2png-0039.png

    Changing the sign of t and rearranging,

    (3.33)2πx(–t)=∫∞–∞X(jΩ)e–jΩtdΩ

    Now if we swap the t and the Ω in Equation 3.33, we arrive at the desired result

    (3.34)2πx(–Ω)=∫∞–∞X(jt)e–jΩtdt

    The right-hand side of Equation 3.34 is recognized as the FT of X(jt), so we have

    (3.35)X(jt)↔2πx(–Ω)

The properties associated with the Fourier Transform are summarized in Table 3.1.

Table 3.1. Fourier Transform properties.
Property y ( t ) Y ( j Ω )
Linearity α x1 ( t ) + β x2 ( t ) α X1 ( j Ω ) + β X2 ( j Ω )
Time Shift x ( t – τ ) X ( j Ω ) e – <
PREV   NEXT